Choice Behavior of Time-Sharing Vehicle Leasing Considering Individual Heterogeneity
-
摘要:
传统交通行为模型缺乏对个体异质性的考虑,导致其对真实选择行为的解释可能存在差距. 为了研究个体异质性对出行选择行为的影响,首先,分别构建了基于混合logit的选择模型以及基于潜在类别条件logit的选择模型;其次,使用正交设计法生成意愿调查问卷,在成都市开展新能源汽车分时租赁的出行选择实证调查;最后,利用极大似然模拟,采用Halton序列抽样对混合logit模型进行标定;采用回归分析对潜在类别条件logit模型进行求解. 结果表明:步行时间、候车时间、车内时间以及出行费用是影响出行方式选择的关键因素,两种模型均反映出个体异质性对出行者选择行为有着显著影响;潜在类别条件logit模型的拟合优度为0.143,优于混合logit模型的0.139,前者命中率为77.85%,也高于后者的61.28%;潜在类别条件logit模型将出行者划分为3个类别,区分度为0.908 4;类别1群体对出行费用最为敏感,对候车时间不敏感;类别2群体对步行时间和候车时间更加敏感,对费用敏感程度较低;类别3群体对时间和费用的敏感程度介于类别1和类别2之间.
Abstract:Lack of individual heterogeneity in traditional travel behavior models causes errors in the interpretation of real choice behaviors. In order to explore the influence of individual heterogeneity on travel choice behavior, firstly, a mixed logit based choice model and a latent-class conditional logit based choice model are built. Secondly, orthogonal design method is used to generate stated preference questionnaires for an empirical survey in Chengdu regarding travel choice behaviors of time-sharing lease on new energy vehicles. Finally, the mixed logit model is calibrated by using maximum likelihood simulation and Halton sequence sampling. The latent-class condition logit model is solved by regression analysis. The results show that access time, waiting time, in-vehicle time and cost are the key factors in choosing urban traffic modes. Both two models reveal that individual heterogeneity has a significant influence on travelers’ choice behaviors. The latent-class conditional logit model has a higher goodness of fit of 0.143 and a hit ratio of 77.85%, compared to those of 0.139 and 61.28% for the mixed logit model. Besides, the latent-class conditional logit model divides travelers into three categories, and the degree of differentiation is 0.908 4. Group 1 is most sensitive to cost but insensitive to waiting time; group 2 is more sensitive to access time and waiting time than cost; group 3 has an intermediate sensitivity to time and cost.
-
异质性最先在遗传学领域被提出,表示遗传物质存在的差异性会导致后代个体在遗传性状的差异. 在交通领域,体异质性理论表述了个体因先天条件或后天环境的差异,个体在外部特性、认知水平、感知态度以及价值观上表现各异,因此,不同出行者之间存在异质性,导致个体面对同一选择情景表现出不同的偏好,亦会面对同一影响因素时表现出敏感程度的差异. 相关研究表明:影响出行者出行选择行为的异质性通常来自于自身,包括可观测的异质性和不可观测的异质性,前者包括出行者性别、收入水平以及小汽车拥有情况等个体社会经济属性,后者主要针对出行者的出行偏好、主观感受以及社会认知等;在出行选择行为研究中是否考虑个体异质性会直接影响分析结果,异质性会通过出行者对交通方式选择的偏好表征出来,从而更好地解释不同群体出行方式的选择偏好,提升模型的拟合优度和解释能力[1-2].
近年来运用在各个领域的考虑个体异质性的模型有很多,如混合logit模型、潜在类别条件logit模型、潜在类别随机参数logit模型以及Hazard模型等[3-11]. 混合logit模型通过将出行属性参数设置为随机参数,依靠随机参数标准偏差探究随机偏好差异,能够在已知的实际选择结果基础上开展对个体级别的偏好估计;潜在类别logit模型通过最佳分类准则将全体样本划分为若干个潜在分类子群体,每个类别群体的参数估计值不同,通过对比不同类别群体之间参数估计值可以分析出不同类别群体间偏好;Hazard模型在进行异质性分析时,考虑时间因素对个体异质性的影响,个体异质性会跟随时间的动态变化,其优势在于能够对不可观测异质性进行测量. 这些模型都可以对个体异质性进行评估,但各模型的适用性未得到充分实证,可以通过不同选择行为问题以及样本进行具体分析,选择最适合的模型.
随着汽车共享与绿色出行相互融合发展,新能源汽车分时租赁逐渐成为一种新兴的出行模式. 本文对新能源汽车分时租赁加入后的城市交通出行方式选择行为进行研究. 为了更加深入地挖掘可观测的异质性对出行选择行为的影响,采用了混合logit模型以及潜在类别条件logit模型来测量个体异质性,既展现每个模型在个体异质性上的表现,也通过对比寻求拟合效果较优的模型,重点分析可观测的异质性所带来的影响,通过出行者个人属性与出行方式属性的交互影响,分析它们之间的偏好关系.
1. 模型构建
首先,确定选择枝集合. 基于目前城市出行中主要的交通出行方式,考虑与新能源汽车分时租赁存在竞争关系的出行方式作为备选项,确定选择枝集合为地铁、常规公交、出租车、私家车、新能源汽车分时租赁. 其次,确定影响选择枝效用的属性,根据实际情况设置步行时间(包括找车)、候车时间、车内时间以及费用作为出行特征属性,同时出行者的性别、年龄、学历、收入和私家车拥有情况等社会经济属性也会影响个体的选择.
1.1 基于混合logit的选择模型
混合logit模型与传统logit不同,模型考虑了个体异质性,能够假设出行者对于出行方式存在偏好差异,模型更加符合实际情况. 通过将出行方式属性参数设置为随机参数测量个体异质性,并能通过模型结果分析个体异质性对选择行为的影响.
在混合logit模型中,出行者
n 选择出行方式i 的效用为{U_{ni}} = {V_{ni}} + {\varepsilon _{ni}}{\kern 1pt} {\text{ = }}\sum\limits_{k = 1}^K {{\beta _{nik}}{x_{nik}} + } {\varepsilon _{ni}}{\text{ = }}{{\boldsymbol{\beta}} }^{\text{T}}_n{{\boldsymbol{X}}_{ni}} + {\varepsilon _{ni}}, (1) 式中:
{V_{ni}} 和{\varepsilon _{ni}}{\kern 1pt} 分别为出行者n选择出行方式i的效用确定项和效用随机项,i=1,2,\cdots,I ;{x_{nik}} 、{\beta _{nik}} 分别为出行者n选择出行方式i的第k种出行相关属性和对应参数; K为出行相关属性的总数;{{\boldsymbol{X}}_{ni}} 为能观测到的出行者n选择出行方式i的属性变量的完整向量,{{\boldsymbol{\beta}} _n} 为对应的参数向量.出行者n选择出行方式i的概率为
{P_{ni}} = \int {{L_{ni}}({{\boldsymbol{\beta}} _n})f\left( {{{\boldsymbol{\beta}} _n}|\theta } \right){\rm{d}}{{\boldsymbol{\beta}} _n}} \text{,} (2) {L_{ni}}\left( {{{\boldsymbol{\beta}} _n}} \right) = \exp \left( {{{\boldsymbol{\beta}} _n}{\boldsymbol{X}_{ni}}} \right)\Bigg/\sum\limits_{i{\text{ = }}1}^I {\exp \left( {{{\boldsymbol{\beta}} _n}{\boldsymbol{X}_{ni}}} \right)} \text{,} (3) 式中:
{L_{ni}}\left({\text{•}}\right) 为多项logit模型中出行者n选择出行方式i的概率;f\left( {{\boldsymbol{\beta} _n}|\theta } \right) 为{\boldsymbol{\beta} _n} 在条件\theta 下的随机参数概率密度函数;\theta 为分布函数的参数.本文将步行时间、候车时间、车内时间及费用对应的参数设置为随机变量,并且服从对数正态分布,则在混合logit模型中,
{V_{ni}} 可表示为{V_{ni}} = {C_{ni}} + \sum\limits_{k = 1}^K {\beta _{nik}^{}x_{nik}^{} + \sum\limits_{j = 1}^J {\beta _{nij}^{}s_{nij}^{}} } \text{,} (4) 式中:
{C_{ni}} 为出行者n选择出行方式i的固有常量;{s_{nij}} 为出行者n选择出行方式i的第j种个人社会经济属性;J 为个人社会经济属性的总数;{\beta _{nik}} 、{\beta _{nij}} 为对应属性的系数.1.2 基于潜在类别条件logit的选择模型
潜在类别条件logit模型能够科学合理地进行样本分类和建模分析,提高行为选择模型精度和解释能力[12-13]. 假设有
N 个出行者,出行选择情景有W 种,每个情景中有I种出行方式,运用潜在类别条件logit模型,根据最佳分类原则将总体样本分为M个不同类别. 若第n个出行者属于m\;(m=1,2,\cdots,M) 类,第m类的出行者n选择第w\;(w=1,2,\cdots,W) 个场景中的交通方式i的总效用为\begin{split} {U_{nwi,m}} = {V_{nwi,m}} + {\varepsilon _{nwi,m}} = {{\boldsymbol{O}}_{nwi,m}^{\rm{T}}}{{\boldsymbol{\xi }}_m} + {\varepsilon _{nwi,m}} \end{split} \text{,} (5) 式中:
{V_{nwi,m}} 、{\varepsilon _{nwi,m}} 和{{\boldsymbol{O}}_{nwi,m}} 分别为第m类的出行者n选择第w个场景中的交通方式i的固定效用、随机效用和出行属性特征向量;{{\boldsymbol{\xi }}_m} 为第m类权重向量.假设出行者n属于第m类选择第w场景中的交通方式i的概率为
{P_{nwi,m}}({{\boldsymbol{\xi }}_m}) = \frac{{\exp \left( {{{\boldsymbol{O}}_{nwi,m}^{\rm{T}}}{{\boldsymbol{\xi }}_m}} \right)}}{{\displaystyle\sum\limits_{i = 1}^I {\exp \left( {{{\boldsymbol{O}}_{nwi,m}^{\rm{T}}}\,{{\boldsymbol{\xi }}_m}} \right)} }} \text{.} (6) 2. 问卷设计与调查
2.1 问卷设计
根据《2019年中国分时租赁行业研究报告》[14]显示,新能源汽车分时租赁出行距离多分布于10 ~20 km的中等距离出行,因此,本文确定以15 km的城市内中距离出行为基础进行问卷设计. 本文结合成都市中心城区客运交通的实际状况,以及新能源汽车分时租赁市场占有率较高的EVCRRD与GOFUN两类品牌收费对各属性的水平值进行设置,属性水平如表1所示,其中,私家车的费用包括油费和停车费. 本文选择正交设计来获得合适的属性组合. 正交设计可以保证各属性的独立性,避免属性的多重线性问题,有效地提高模型结果的精度. 本文利用正交设计,通过均衡搭配形成具有代表性和典型性的属性水平组合,最终生成16个选择情境组成一套问卷. 同时问卷采集了受访者的个人社会经济属性. 个人属性水平与编码设置如表2所示.
表 1 选择枝属性水平Table 1. Levels of alternative attributes出行方式 属性 水平 1 水平 2 地铁 步行时间/min 15 20 候车时间/min 2 5 车内时间/min 35 35 费用/元 5 5 公交 步行时间/min 10 16 候车时间/min 10 15 车内时间/min 50 64 费用/元 2 2 出租车 步行时间/min 2 3 候车时间/min 4 8 车内时间/min 30 45 费用/元 38 42 私家车 步行时间/min 5 8 车内时间/min 30 45 费用/元 15 20 新能源汽车
分时租赁步行时间/min 15 20 候车时间/min 0 0 车内时间/min 30 45 费用/元 17 24 表 2 个人属性水平及编码Table 2. Levels of individual attribute and coding变量 个人属性水平 编码 性别 男 1 女 2 年龄 18 岁 ~ 25 岁 1 26 岁 ~ 30 岁 2 31 岁 ~ 35 岁 3 36 岁 ~ 40 岁 4 41 岁 ~ 45 岁 5 45 岁 ~ 50 岁 6 51 岁 ~ 55 岁 7 > 55 岁 8 学历 初中及以下 1 高中/中专/技校 2 大专 3 本科 4 研究生及以上 5 月收入 > 3000 元 1 3000 ~ 5000 元 2 5001 ~ 8000 元 3 8001 ~ 10000 元 4 > 10000 元 5 拥有私家车 拥有 1 未拥有 2 2.2 调查开展与样本分析
本文在成都市开展问卷调查,共收集有效样本378份. 对有效样本进行整理分析,结果如表3所示. 有效样本中,男性占比46.0%,女性占比54.0%,基本符合人口调查比例. 年龄分布占比最多的是31岁 ~35岁,总体集中在18岁~ 40岁,较为符合新能源汽车分时租赁使用偏向中青年群体的特征. 受访者的收入主要集中在5000 ~ 10000元/月. 调查样本的年龄、性别与收入分布与抽样计划基本一致.
表 3 样本个人属性统计Table 3. Statistical results for individual attribute of surveyed samples调查内容 选项 样本数/份 比例/% 性别 男 174 46.0 女 204 54.0 年龄 18 岁 ~ 25 岁 61 16.1 26 岁 ~ 30 岁 83 22.0 31 岁 ~ 35 岁 115 30.4 36 岁 ~ 40 岁 64 16.9 41 岁 ~ 45 岁 26 6.9 45 岁 ~ 50 岁 25 6.6 51 岁 ~ 55 岁 4 1.1 > 55 岁 0 0 学历 初中及以下 8 2.1 高中/中专/技校 26 6.9 大专 67 17.7 本科 247 65.3 研究生及以上 30 7.9 职业 企业员工 223 59.0 商业/服务业人员 27 7.1 机关/事业单位人员 67 17.7 学生 53 14.0 其他 8 2.1 月收入 > 3000 元 59 15.6 3000 ~ 5000 元 59 15.6 5000 ~ 8000 元 126 33.3 8000 ~ 10000 元 87 23.0 > 10000 元 47 12.4 是否拥有
私家车有 261 69.0 没有 117 31.0 3. 结果分析
3.1 混合logit模型标定结果及分析
本文借助NLogit 4.0,利用极大似然模拟,采用Halton序列抽样,对混合logit模型进行标定,抽取总次数为500次时模型估计结果稳定,具体步骤为:
步骤1 已知对应参数的联合概率密度函数
f\left( {{\boldsymbol{\beta} _n}{\text{|}}\theta } \right) 分布形式,给定\theta 值,用Halton抽样法从密度函数中抽取一个随机向量,记为\boldsymbol{\beta} _n^{(r)} ,r为抽取次数,第一次抽取,r = 1 .步骤2 利用式(3)计算本次抽样的概率值
{L_{ni}}\left( {\boldsymbol{\beta} _n^{(r)}} \right) .步骤3 重复步骤1、2共R次,R = 500. 计算
{L_{ni}}\left( {\boldsymbol{\beta} _n^{(r)}} \right) 的均值作为近似概率来给出模拟概率{P_{ni}} ,即{P_{ni}}{\text{ = }}\frac{1}{R}\sum\limits_{r = 1}^R {{L_{ni}}\left( {\boldsymbol{\beta} _n^{(r)}} \right)} . (7) 步骤4 本文样本为378份,出行方式为5个,构造样本的似然函数
G\left( {{\boldsymbol{\beta} _n}} \right) 为G\left( {{\boldsymbol{\beta} _n}} \right) = \prod\limits_{n=1}^{378} {\prod\limits_{i=1}^5 {P_{ni}^{{y_{ni}}}} } \text{,} (8) 式中:
{y_{{ni}}} 为0-1变量,当个体n 选择方案为 i 时,{y_{^{ni}}} 为1,否则为0.取式(8)的对数形式得到模拟极大似然算子为
K\left( {{\boldsymbol{\beta} _n}} \right) = \prod\limits_{n=1}^{378} {\prod\limits_{i=1}^5 {{y_{ni}}\ln {{P_{ni}}} } } . (9) 可以证明式(9)是关于
{\beta _n} 的凸函数,因此令K\left( {{\boldsymbol{\beta} _n}} \right) 对{\boldsymbol{\beta} _n} 的导数向量为0, 此时达到最大值,求得其极大似然估计值.步骤5 改变
\theta 值,重复计算步骤1 ~ 4,直到模拟极大似然算子取得最大值.标定结果如表4所示. 通过P值检验各参数的显著性. 标定结果中,性别参数符号为正表示女性,参数符号为负表示男性;年龄、学历以及收入参数符号为正分别表示年龄越大、学历以及收入水平越高;而私家车拥有参数符号为正表示未拥有私家车,参数符号为负表示拥有私家车.
表 4 混合logit模型参数标定结果Table 4. Calibration results of mixed logit model属性 参数值 标准误差 P 值 步行时间 −0.0723① 0.01441 0 候车时间 −0.0447② 0.02036 0.028 车内时间 −0.0198① 0.00478 0 费用 −0.0207② 0.00998 0.038 步行时间标准差 0.0451② 0.20413 0.271 候车时间标准差 0.0315② 0.01723 0.068 车内时间标准差 0.0109③ 0.00587 0.064 费用标准差 0.0165② 0.00826 0.046 地铁固有常量 0.4389① 0.08190 0 公交固有常量 −0.5564② 0.25027 0.026 出租车固有常量 −0.7516② 0.38028 0.048 新能源汽车分时
租赁固有常量0.3935③ 0.22469 0.080 性别 0.1866 0.12011 0.120 年龄 0.2437② 0.12708 0.055 收入 −0.5649① 0.05821 0 学历 0.0976 0.83657 0.244 是否拥有私家车 −1.4824① 0.15972 0 注:①、②、③分别表示在1%、5%、10%下显著,后同. 由表4可以看出:
1) 公交、地铁、出租车和新能源汽车分时租赁4种选择枝的固定参数均显著,说明这4种方式未被观测到效用对其总效用各有影响. 新能源汽车分时租赁和出租车固定常数均显著,但前者参数符号为正,后者参数符号为负,说明相比于私家车出行,新能源汽车分时租赁具有一定的优势能够让部分私家车出行转移到新能源汽车分时租赁,出租车相对于私家车优势不明显.
2) 年龄、收入和是否拥有小汽车3个参数均显著. 其中,年龄参数符号为正,收入与是否拥有小汽车参数符号为负,表明年龄越大的出行者对地铁或者公交出行存在偏好,使用新能源汽车分时租赁的年轻群体更多,而收入较高的有车群体更愿意选择私家车出行.
3) 步行时间、候车时间、车内时间以及费用4个变量均显著且符号均为负,说明这4个变量值越高选择该交通方式的概率越低,符合实际情况. 其中,步行时间参数值绝对值最大,说明步行时间是影响出行方式选择较为重要的因素.
混合logit模型输出的属性变量的标准差值均显著,说明不同个体具有不同于样本均值参数估计的个体异质性. 为了分析个体异质性的可能来源,本文假设设置的随机参数异质性来源于个体社会经济属性的差异,通过使各随机参数与个体经济属性相互作用来确定. 本文利用NLogit软件分析个人经济社会属性与选择方案属性之间相互作用,得到的交互效应结果如表5所示. 首先,分析个体收入属性. “步行时间-收入”、“候车时间-收入”和“车内时间-收入”交互作用显著且呈正相关,说明收入越高的群体对步行时间、车内时间和候车时间增加更加敏感. 同时,“费用-收入”交互作用结果显著,符号为正,说明收入越高的群体对出行费用增加表现不敏感;综上,在个体异质性上收入越高的群体相比于出行费用更加注重时间价值,尤其是通勤出行时注重交通方式两端接驳的便利性,因此,更加合理和密集的租赁站点能够吸引这部分人群使用新能源汽车分时租赁. 同理分析个体私家车拥有属性. 步行时间、候车时间与私家车拥有情况交互作用显著,呈负相关,说明无车群体对步行时间和候车时间的增加表现不敏感,符合无车群体出行时多选择地铁、公交等传统公共交通方式的事实. “费用-拥车”交互参数显著且正相关,说明无车群体对于费用增加表现比较敏感,更偏好于公共交通出行. 新能源汽车分时租赁步行、候车时间比传统公共交通短,比私家车长,出行费用比传统公共交通高但比私家车便宜,更能吸引无车群体的使用.
表 5 个体社会经济属性与出行方案属性交互分析Table 5. Interaction analysis of individual social-demographic attributes and travel mode statistics交互属性 参数值 标准误差 z 值 P 值 步行时间-性别 −0.0150 0.01650 −0.91 0.362 步行时间-年龄 0.0017 0.00602 0.28 0.776 步行时间-学历 −0.0026 0.01105 −0.24 0.813 步行时间-拥车 0.1134① 0.01901 5.97 0 步行时间-收入 −0.0254① 0.00898 −2.83 0.005 候车时间-性别 −0.0007 0.01723 −0.04 0.966 候车时间-年龄 −0.0059 0.00640 −0.92 0.359 候车时间-学历 0.3591 0.01146 −0.30 0.763 候车时间-拥车 0.1071① 0.02051 5.22 0 候车时间-收入 −0.0579① 0.00929 −6.23 0 车内时间-性别 0.0079 0.00840 0.94 0.345 车内时间-年龄 0.0030 0.00308 0.96 0.338 车内时间-学历 −0.0101③ 0.00545 −1.85 0.064 车内时间-拥车 −0.0063 0.00951 −0.66 0.507 车内时间-收入 −0.0096② 0.00431 −2.23 0.026 费用-性别 0.0038 0.00805 0.47 0.642 费用-年龄 0.0028 0.00295 0.95 0.340 费用-学历 −0.0023 0.00549 −0.42 0.676 费用-拥车 −0.0373① 0.00912 −4.09 0 费用-收入 0.0355① 0.00430 8.25 0 3.2 潜在类别条件logit模型标定结果及分析
潜在类别条件logit模型进行出行方式选择行为分析的第一步是确定出行者的最佳分类数. 最佳分类数的确定基于定量与定性的考虑,通过一致的赤池信息准则 (consistent Akaike information criterion,CAIC)和贝叶斯信息准则 (Bayesian information criterion,BIC)定量确定最佳的潜在类别数量,CAIC值和BIC值越小,模型拟合度越高. 实际运用时通过设置一个最大的分类数量,然后利用潜在类别条件logit模型对每个分类数量下的样本进行回归,从而获取每个类别数量对应的CAIC和BIC,一般情况选取CAIC和BIC最小时的分类数作为最佳的潜在类别数量,当无法同时满足时,通常取CAIC最小值的分类数作为最佳分类数. CAIC 和BIC分别为
{Q_{\rm{CAIC}}} = - 2 D + h(1 + \ln \;N), (10) {Q_{\rm{BIC}}}= - 2 D + h\ln\; N , (11) 式中:D为样本最大对数似然值;h为拟合模型参数的总数量.
运用stata编程得到不同分类数的CAIC以及BIC, 结果如表6所示,表中,LLF为对数似然值.
表 6 潜在类别条件logit模型分类结果Table 6. Classification results of latent-class conditional logit model类别 LLF CAIC BIC 2 −1978.08 4053.238 4039.238 3 −1899.77 3959.967 3912.967 4 −1862.93 3961.655 3927.655 5 −1849.01 4003.150 3959.150 6 −1833.14 4040.768 3959.150 7 −1822.50 4088.827 4024.827 8 −1815.94 4145.058 4071.058 由表6可知:当潜在类别的数目增多时,模型适配LLF绝对值也在下降,当分类数为3时,其CAIC和BIC均为最小值,说明最佳潜在类别数量为3,因此,将通勤选择模型的样本划分为3个类别. 对样本进行潜在类别条件logit模型回归,结果如表7所示.
由表7可知:步行时间、候车时间、车内时间以及费用4个变量参数值符号均为负,与混合logit模型结果一致,但不同参数估计值在不同类别中显著性各异,说明不同类别的出行者在对出行方式选择的偏好程度上表现出了较强的异质性. 具体分析如下:
表 7 潜在类别条件logit模型回归结果Table 7. Regression results of latent-class conditional logit model类别 属性 参数值 标准差 z 值 P 值 步行时间 −0.2000① 0.045527 −4.40 0 1 候车时间 −0.0508 0.052150 −0.97 0.330 车内时间 −0.0496② 0.020274 −2.45 0.014 费用 −0.4654① 0.107002 −4.35 0 2 步行时间 −0.1776① 0.015585 −11.40 0 候车时间 −0.2419① 0.019889 −12.16 0 车内时间 −0.0246① 0.007539 −3.27 0.001 费用 −0.0050 0.007848 −0.64 0.523 3 步行时间 −0.0330① 0.011412 −2.89 0.004 候车时间 −0.0657① 0.015323 −4.29 0 车内时间 −0.0381① 0.006395 −5.96 0 费用 −0.0446① 0.006366 −7.00 0 1) 类别1群体中步行时间和费用参数显著,候车时间参数不显著,费用参数绝对值为3个类别中最大,说明类别1群体属于“费用敏感型”,能够接受较长的候车时间,但不太能接受费用的增加,这类群体更偏好于选择地铁或公交出行.
2) 类别2群体中步行时间与候车时间参数显著且绝对值较大,费用参数不显著,说明类别2群体属于“时间敏感型”. 这类群体出行时对时间因素更加关注,而对费用敏感程度不高,更偏好于私家车或出租车出行. 新能源汽车分时租赁也属于小汽车出行,通过提升车辆品质以及个性化服务能够提升其对类别2群体的吸引力.
3) 类别3群体中4参数均显著,参数绝对值都介于类别1和类别2之间,属于“出行平衡型”. 这类出行者选择交通方式时会同时关注时间和费用因素,不会对某一因素特别敏感,希望在各个出行属性上寻求平衡,而新能源汽车分时租赁服务特性能较好满足这类群体出行需求.
将类别3作为参考基准,出行者特性对潜在类别的影响如表8所示. 由表可知:固定常数在类别1中不显著,在类别2中显著且符号为负,说明未观测到的固定效用对类别2的出行方式选择有抑制作用,类别2的群体有向类别3转移的可能;性别和年龄在类别1中均不显著,在类别2中均显著,且性别参数符号为正,年龄参数符号为负,即在类别2中女性更加愿意选择类别2群体所偏爱的私家车或出租车,且类别2群体随着年龄的增加,越不容易成为“时间敏感型”,因此,类别2中,年龄越大的女性可能更容易被能够提供优质服务的新能源汽车分时租赁所吸引;学历在类别1中显著且符号为负,在类别2中不显著,说明在类别1中,学历越高越不容易成为“费用敏感型”;收入在类别1和类别2中均显著,但前者参数符号为负,后者为正,说明收入越高对时间越敏感.
表 8 出行者特性对潜在类别的影响Table 8. Influence of travelers’ characteristics on latent class类别 属性 参数值 标准差 z 值 P 值 1 性别 0.5523 0.388434 1.42 0.155 年龄 −0.3348 0.453656 −0.74 0.461 学历 −0.7091③ 0.389555 −1.82 0.069 收入 −0.7178③ 0.412547 −1.74 0.082 是否拥
有私家车1.3281① 0.390433 3.40 0.001 固定常数 0.5060 0.310452 1.63 0.103 2 性别 0.9755② 0.481793 2.02 0.043 年龄 −0.9951② 0.489439 −2.03 0.042 学历 0.5408 0.614215 0.88 0.379 收入 0.8241① 0.266693 3.09 0.002 是否拥有私家车 −3.0222② 0.834863 −3.62 0.001 固定常数 −2.4347① 0.922243 −2.64 0.008 3.3 模型对比分析
通过计算得到混合logit模型和潜在类别条件logit模型的拟合优度和命中率如表9所示. 两个模型的各参数检验效果较好,具有一定的解释力,都是考虑个体异质性的出行选择行为模型. 由表可知:潜在类别条件logit模型的拟合优度比混合logit模型提高了0.04,潜在类别条件logit模型的拟合效果更好. 潜在类别条件logit模型的命中率比混合logit模型的命中率高16.57%,说明潜在类别条件logit模型对全体样本进行分类标定,对预测不同偏好的群体的选择行为有一定的优势;潜在类别条件logit模型对出行者进行了类别区分,区分度为0.9084,能较好地对全样本群体进行群体偏好性区分,通过最佳分类数将出行者划分为不同群体,并同时对每一类群体进行标定,分析参数标定结果可以明确不同种类的特征以及出行偏好. 综上所述,相较于混合logit模型,潜在类别logit模型拟合效果更好,模型解释力更强,对预测不同偏好群体的新能源汽车分时租赁选择行为具有一定的优势.
表 9 模型对比分析Table 9. Model comparison analysis项目 混合 logit 潜在类别条件 logit 拟合优度 0.139 0.143 命中率/% 61.28 77.85 区分度 0.9084 4. 结 论
本文以成都市实际调查数据为基础,分别建立了基于混合logit以及基于潜在类别条件logit的选择模型分析考虑异质性的新能源汽车分时租赁选择行为,对相关属性变量参数进行了显著性分析,并对两种模型进行了对比,所得主要结论总结如下:
1) 步行时间、候车时间、车内时间以及费用均对新能源汽车分时租赁选择行为有着重要影响,但不同的出行者对时间和费用的敏感程度不同,表现出不同的个体偏好性. 其中,步行时间对出行者选择影响最为显著. 新能源汽车分时租赁应该合理地提升租赁站点的密集度、增加可供租赁的车辆数,减少步行和找车时间以吸引更多出行者.
2) 收入、性别、学历及私家车拥有情况等个人属性对不同类别出行者的选择行为有着不同的影响. 新能源汽车分时租赁可以考虑提供差异化服务丰富出行者的选择,吸引不同类别的群体. 例如可以提供更高档更舒适的车型以吸引部分高收入、高学历以及拥有私家车的人群使用,这部分群体对费用不是特别关注,更关注出行时间和品质.
3) 相较于混合logit模型,潜在类别条件logit模型拟合优度提高了0.004,命中率提高了16.57%,模型解释力更强,能更好地考虑个体异质性对新能源汽车分时租赁选择行为的影响,分析不同类别群体的选择偏好.
-
表 1 选择枝属性水平
Table 1. Levels of alternative attributes
出行方式 属性 水平 1 水平 2 地铁 步行时间/min 15 20 候车时间/min 2 5 车内时间/min 35 35 费用/元 5 5 公交 步行时间/min 10 16 候车时间/min 10 15 车内时间/min 50 64 费用/元 2 2 出租车 步行时间/min 2 3 候车时间/min 4 8 车内时间/min 30 45 费用/元 38 42 私家车 步行时间/min 5 8 车内时间/min 30 45 费用/元 15 20 新能源汽车
分时租赁步行时间/min 15 20 候车时间/min 0 0 车内时间/min 30 45 费用/元 17 24 表 2 个人属性水平及编码
Table 2. Levels of individual attribute and coding
变量 个人属性水平 编码 性别 男 1 女 2 年龄 18 岁 ~ 25 岁 1 26 岁 ~ 30 岁 2 31 岁 ~ 35 岁 3 36 岁 ~ 40 岁 4 41 岁 ~ 45 岁 5 45 岁 ~ 50 岁 6 51 岁 ~ 55 岁 7 > 55 岁 8 学历 初中及以下 1 高中/中专/技校 2 大专 3 本科 4 研究生及以上 5 月收入 > 3000 元 1 3000 ~ 5000 元 2 5001 ~ 8000 元 3 8001 ~ 10000 元 4 > 10000 元 5 拥有私家车 拥有 1 未拥有 2 表 3 样本个人属性统计
Table 3. Statistical results for individual attribute of surveyed samples
调查内容 选项 样本数/份 比例/% 性别 男 174 46.0 女 204 54.0 年龄 18 岁 ~ 25 岁 61 16.1 26 岁 ~ 30 岁 83 22.0 31 岁 ~ 35 岁 115 30.4 36 岁 ~ 40 岁 64 16.9 41 岁 ~ 45 岁 26 6.9 45 岁 ~ 50 岁 25 6.6 51 岁 ~ 55 岁 4 1.1 > 55 岁 0 0 学历 初中及以下 8 2.1 高中/中专/技校 26 6.9 大专 67 17.7 本科 247 65.3 研究生及以上 30 7.9 职业 企业员工 223 59.0 商业/服务业人员 27 7.1 机关/事业单位人员 67 17.7 学生 53 14.0 其他 8 2.1 月收入 > 3000 元 59 15.6 3000 ~ 5000 元 59 15.6 5000 ~ 8000 元 126 33.3 8000 ~ 10000 元 87 23.0 > 10000 元 47 12.4 是否拥有
私家车有 261 69.0 没有 117 31.0 表 4 混合logit模型参数标定结果
Table 4. Calibration results of mixed logit model
属性 参数值 标准误差 P 值 步行时间 −0.0723① 0.01441 0 候车时间 −0.0447② 0.02036 0.028 车内时间 −0.0198① 0.00478 0 费用 −0.0207② 0.00998 0.038 步行时间标准差 0.0451② 0.20413 0.271 候车时间标准差 0.0315② 0.01723 0.068 车内时间标准差 0.0109③ 0.00587 0.064 费用标准差 0.0165② 0.00826 0.046 地铁固有常量 0.4389① 0.08190 0 公交固有常量 −0.5564② 0.25027 0.026 出租车固有常量 −0.7516② 0.38028 0.048 新能源汽车分时
租赁固有常量0.3935③ 0.22469 0.080 性别 0.1866 0.12011 0.120 年龄 0.2437② 0.12708 0.055 收入 −0.5649① 0.05821 0 学历 0.0976 0.83657 0.244 是否拥有私家车 −1.4824① 0.15972 0 注:①、②、③分别表示在1%、5%、10%下显著,后同. 表 5 个体社会经济属性与出行方案属性交互分析
Table 5. Interaction analysis of individual social-demographic attributes and travel mode statistics
交互属性 参数值 标准误差 z 值 P 值 步行时间-性别 −0.0150 0.01650 −0.91 0.362 步行时间-年龄 0.0017 0.00602 0.28 0.776 步行时间-学历 −0.0026 0.01105 −0.24 0.813 步行时间-拥车 0.1134① 0.01901 5.97 0 步行时间-收入 −0.0254① 0.00898 −2.83 0.005 候车时间-性别 −0.0007 0.01723 −0.04 0.966 候车时间-年龄 −0.0059 0.00640 −0.92 0.359 候车时间-学历 0.3591 0.01146 −0.30 0.763 候车时间-拥车 0.1071① 0.02051 5.22 0 候车时间-收入 −0.0579① 0.00929 −6.23 0 车内时间-性别 0.0079 0.00840 0.94 0.345 车内时间-年龄 0.0030 0.00308 0.96 0.338 车内时间-学历 −0.0101③ 0.00545 −1.85 0.064 车内时间-拥车 −0.0063 0.00951 −0.66 0.507 车内时间-收入 −0.0096② 0.00431 −2.23 0.026 费用-性别 0.0038 0.00805 0.47 0.642 费用-年龄 0.0028 0.00295 0.95 0.340 费用-学历 −0.0023 0.00549 −0.42 0.676 费用-拥车 −0.0373① 0.00912 −4.09 0 费用-收入 0.0355① 0.00430 8.25 0 表 6 潜在类别条件logit模型分类结果
Table 6. Classification results of latent-class conditional logit model
类别 LLF CAIC BIC 2 −1978.08 4053.238 4039.238 3 −1899.77 3959.967 3912.967 4 −1862.93 3961.655 3927.655 5 −1849.01 4003.150 3959.150 6 −1833.14 4040.768 3959.150 7 −1822.50 4088.827 4024.827 8 −1815.94 4145.058 4071.058 表 7 潜在类别条件logit模型回归结果
Table 7. Regression results of latent-class conditional logit model
类别 属性 参数值 标准差 z 值 P 值 步行时间 −0.2000① 0.045527 −4.40 0 1 候车时间 −0.0508 0.052150 −0.97 0.330 车内时间 −0.0496② 0.020274 −2.45 0.014 费用 −0.4654① 0.107002 −4.35 0 2 步行时间 −0.1776① 0.015585 −11.40 0 候车时间 −0.2419① 0.019889 −12.16 0 车内时间 −0.0246① 0.007539 −3.27 0.001 费用 −0.0050 0.007848 −0.64 0.523 3 步行时间 −0.0330① 0.011412 −2.89 0.004 候车时间 −0.0657① 0.015323 −4.29 0 车内时间 −0.0381① 0.006395 −5.96 0 费用 −0.0446① 0.006366 −7.00 0 表 8 出行者特性对潜在类别的影响
Table 8. Influence of travelers’ characteristics on latent class
类别 属性 参数值 标准差 z 值 P 值 1 性别 0.5523 0.388434 1.42 0.155 年龄 −0.3348 0.453656 −0.74 0.461 学历 −0.7091③ 0.389555 −1.82 0.069 收入 −0.7178③ 0.412547 −1.74 0.082 是否拥
有私家车1.3281① 0.390433 3.40 0.001 固定常数 0.5060 0.310452 1.63 0.103 2 性别 0.9755② 0.481793 2.02 0.043 年龄 −0.9951② 0.489439 −2.03 0.042 学历 0.5408 0.614215 0.88 0.379 收入 0.8241① 0.266693 3.09 0.002 是否拥有私家车 −3.0222② 0.834863 −3.62 0.001 固定常数 −2.4347① 0.922243 −2.64 0.008 表 9 模型对比分析
Table 9. Model comparison analysis
项目 混合 logit 潜在类别条件 logit 拟合优度 0.139 0.143 命中率/% 61.28 77.85 区分度 0.9084 -
[1] BALBONTIN C, HENSHER D A, COLLINS A T. How to better represent preferences in choice models: the contributions to preference heterogeneity attributable to the presence of process heterogeneity[J]. Transportation Research Part B: Methodological, 2019, 122: 218-248. doi: 10.1016/j.trb.2019.02.007 [2] HESS S, STATHOPOULOS A, DALY A. Allowing for heterogeneous decision rules in discrete choice models: an approach and four case studies[J]. Transportation, 2012, 39(3): 565-591. doi: 10.1007/s11116-011-9365-6 [3] MANNERING F L, SHANKAR V, BHAT C R. Unobserved heterogeneity and the statistical analysis of highway accident data[J]. Analytic Methods in Accident Research, 2016, 11: 1-16. doi: 10.1016/j.amar.2016.04.001 [4] IBEAS A, DELL’OLIO L, BORDAGARAY M, et al. Modelling parking choices considering user heterogeneity[J]. Transportation Research Part A: Policy and Practice, 2014, 70: 41-49. doi: 10.1016/j.tra.2014.10.001 [5] DUAN L W, PENG Q Y, TANG Y Y. Railway shippers’ heterogeneous preferences with random parameters latent class model[J]. Transportation Research Procedia, 2017, 25: 416-424. doi: 10.1016/j.trpro.2017.05.419 [6] 赵鹏,翟茹雪,宋文波. 考虑个体异质性的高速铁路旅客选择行为[J]. 北京交通大学学报,2019,43(2): 117-123. doi: 10.11860/j.issn.1673-0291.20180127ZHAO Peng, ZHAI Ruxue, SONG Wenbo. Passenger choice behavior of high-speed railway considering individual heterogeneity[J]. Journal of Beijing Jiaotong University, 2019, 43(2): 117-123. doi: 10.11860/j.issn.1673-0291.20180127 [7] GREENE W H, HENSHER D A. A latent class model for discrete choice analysis: contrasts with mixed logit[J]. Transportation Research Part B: Methodological, 2003, 37(8): 681-698. doi: 10.1016/S0191-2615(02)00046-2 [8] GREENE W H, HENSHER D A. Revealing additional dimensions of preference heterogeneity in a latent class mixed multinomial logit model[J]. Applied Economics, 2013, 45(14): 1897-1902. doi: 10.1080/00036846.2011.650325 [9] 刘志伟,刘建荣,邓卫. 考虑潜在类别的市内机动化出行行为模型[J]. 西南交通大学学报,2021,56(1): 131-137.LIU Zhiwei, LIU Jianrong, DENG Wei. Inclusion of latent class in behavior model of motorized travel in city[J]. Journal of Southwest Jiaotong University, 2021, 56(1): 131-137. [10] 刘志伟,刘建荣,邓卫. 无人驾驶汽车对出行方式选择行为的影响[J]. 西南交通大学学报,2021,56(6): 1161-1168.LIU Zhiwei, LIU Jianrong, DENG Wei. Impact of autonomous vehicle on travel mode choice behavior[J]. Journal of Southwest Jiaotong University, 2021, 56(6): 1161-1168. [11] 姚荣涵,杨澜,王仲. 考虑潜变量的自动驾驶汽车租赁行为[J]. 西南交通大学学报,2021,56(6): 1153-1160.YAO Ronghan, YANG Lan, WANG Zhong. Leasing behavior for autonomous vehicles considering latent variables[J]. Journal of Southwest Jiaotong University, 2021, 56(6): 1153-1160. [12] HURTUBIA R, NGUYEN M H, GLERUM A, et al. Integrating psychometric indicators in latent class choice models[J]. Transportation Research Part A: Policy and Practice, 2014, 64: 135-146. doi: 10.1016/j.tra.2014.03.010 [13] BAE Y, KIM J, CHUNG J. Psychological traits to eco-friendly transportation systems:latent class approach[J]. Transportation Research Procedia, 2017, 25: 4270-4284. doi: 10.1016/j.trpro.2017.05.246 [14] 艾瑞咨询. 2019年中国分时租赁行业研究报告 [R/OL]. (2019-03-20) [2020-06-22]. http://report.iresearch.cn/wx/report.aspx?id=3347. 期刊类型引用(5)
1. 杨婷群,陈坚. 考虑铁路旅客偏好差异的离站方式选择行为分析. 交通运输研究. 2024(03): 1-9 .  百度学术
百度学术2. 孙小慧,王飞燕. 考虑心理潜变量的共享电动汽车选择意向. 公路工程. 2023(05): 174-180+191 .  百度学术
百度学术3. 万谧宇,敖宇兴,柳键. 基于演化博弈的汽车分时租赁出行模式决策研究. 科技创业月刊. 2023(11): 40-44 .  百度学术
百度学术4. 杨亚璪,唐浩冬,彭勇. 考虑偏好差异的后疫情时代居民出行方式选择行为研究. 交通运输系统工程与信息. 2022(03): 15-24 .  百度学术
百度学术5. 万明,梁莹,周涂强,严利鑫,郭军华,李芳源. 考虑动态交通信息的异质出行行为分析. 华东交通大学学报. 2022(05): 61-69 .  百度学术
百度学术其他类型引用(12)
-

 点击查看大图
点击查看大图
计量
- 文章访问数: 429
- HTML全文浏览量: 178
- PDF下载量: 18
- 被引次数: 17




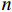
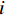
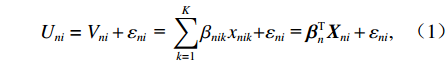
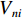
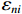
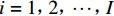
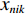
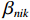
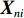
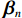
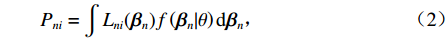
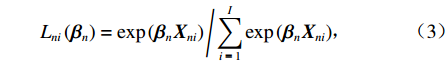
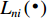
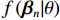
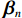
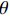
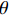
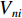
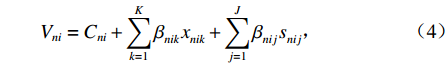
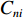
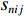
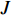
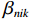
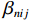
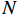
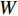
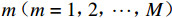
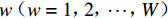
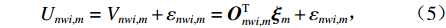
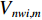


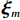
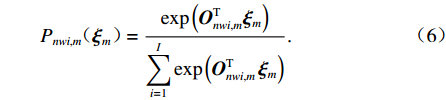
 下载:
下载:
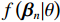
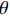
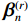

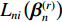
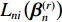
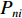
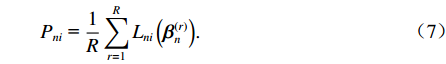
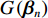
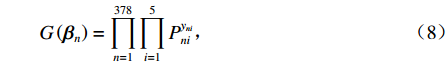
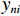
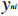
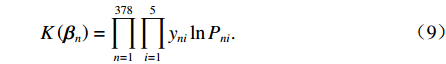
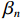
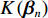
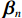
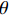
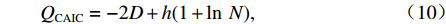

 下载:
下载:  百度学术
百度学术