Effects of Strength Degradation of Sliding Mass on Movement of Vajont Landslide Numerical Simulation Based on Discontinuous Deformation Analysis
-
摘要:
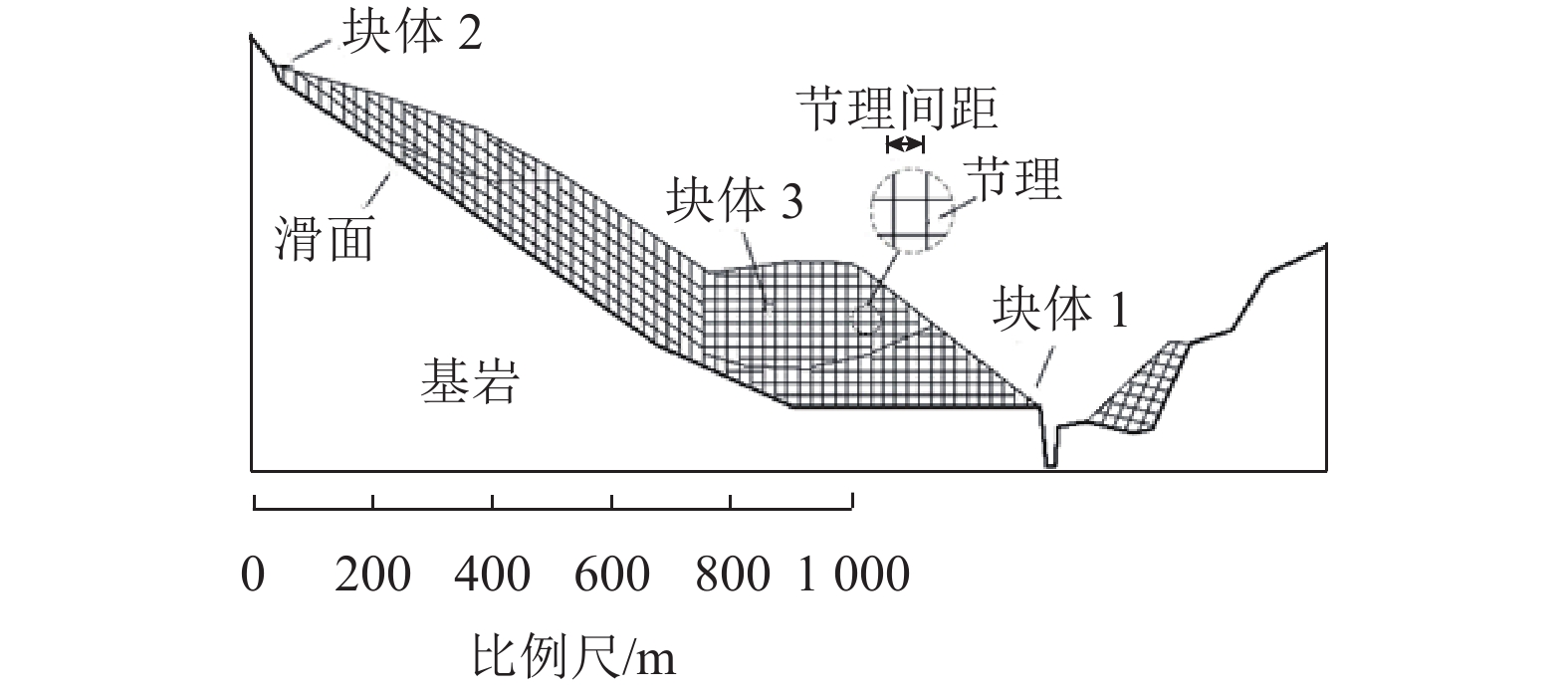
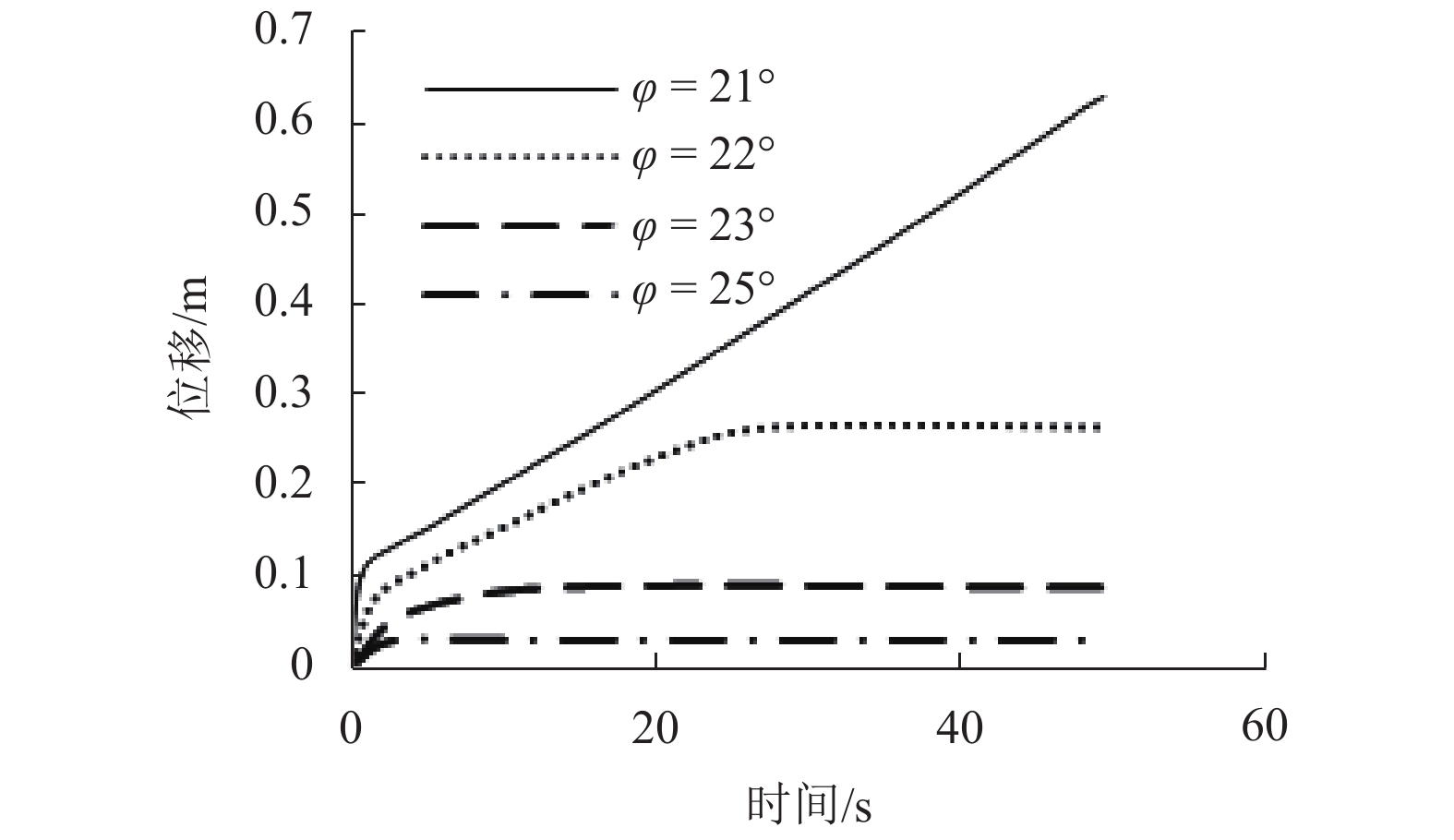
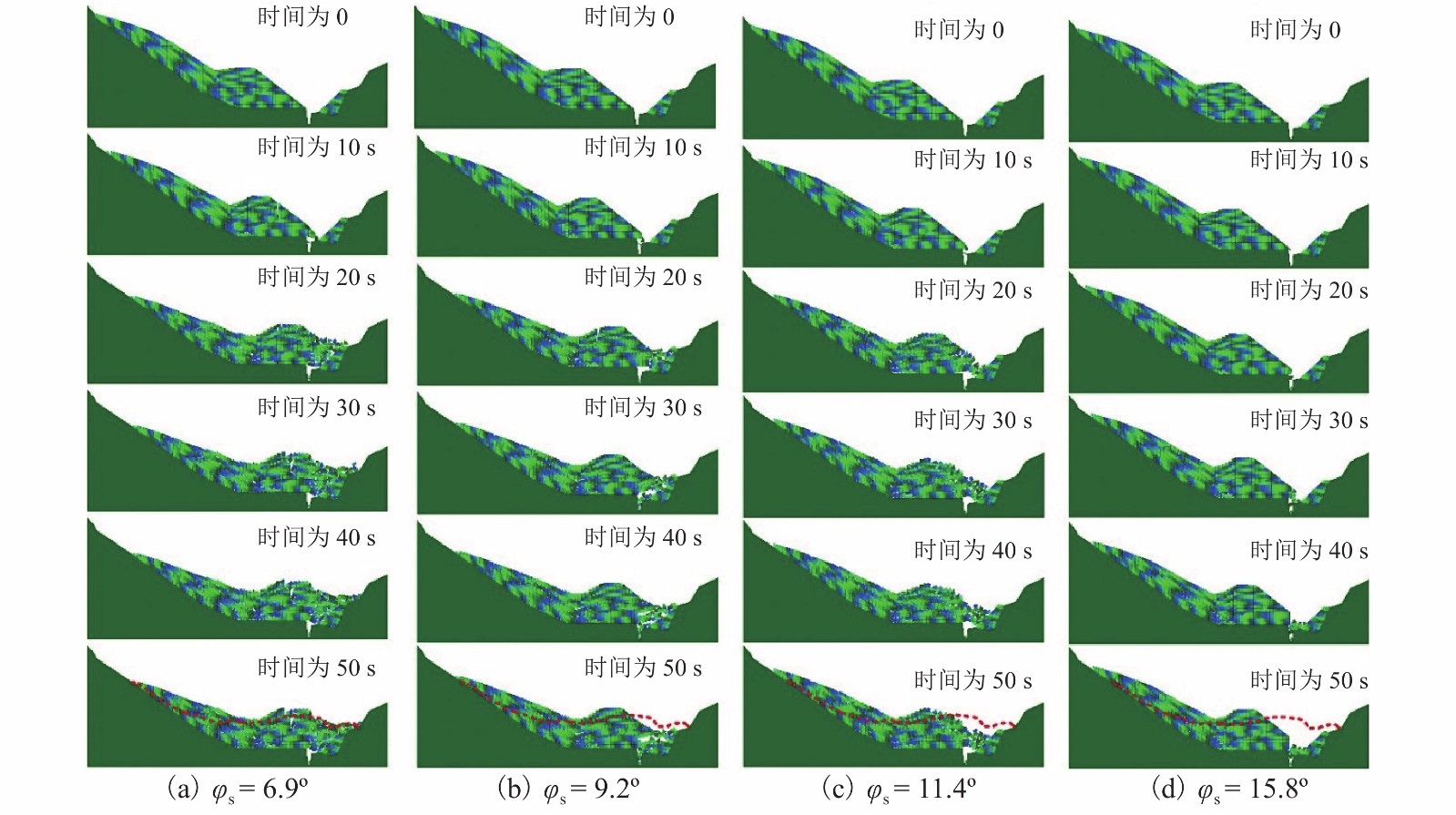
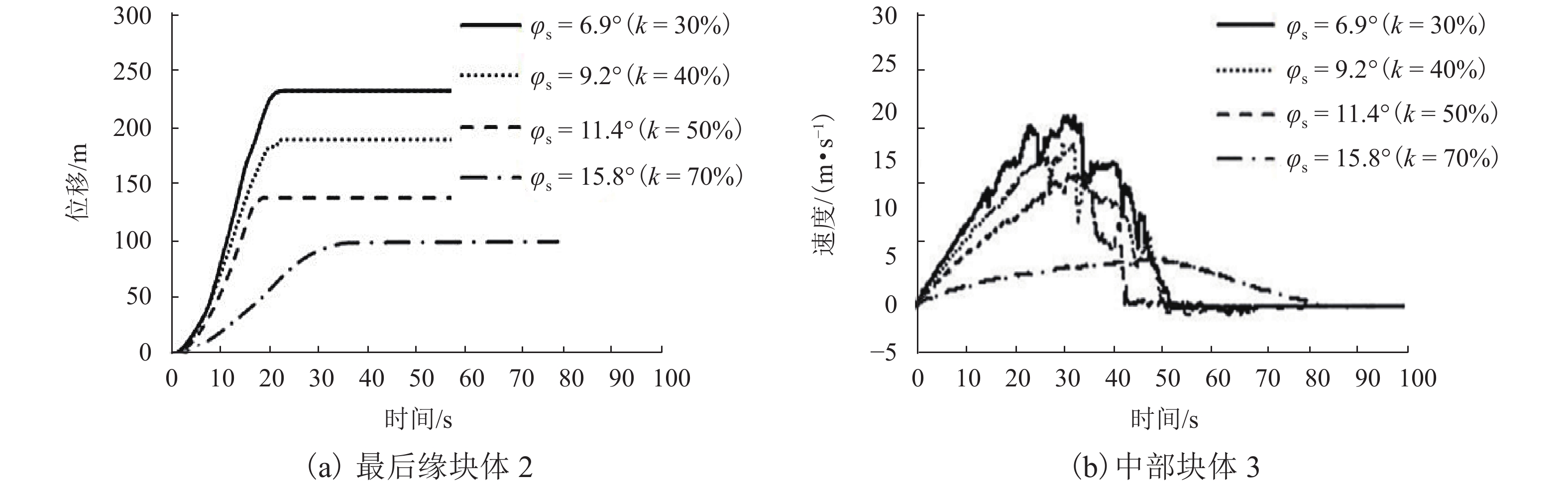
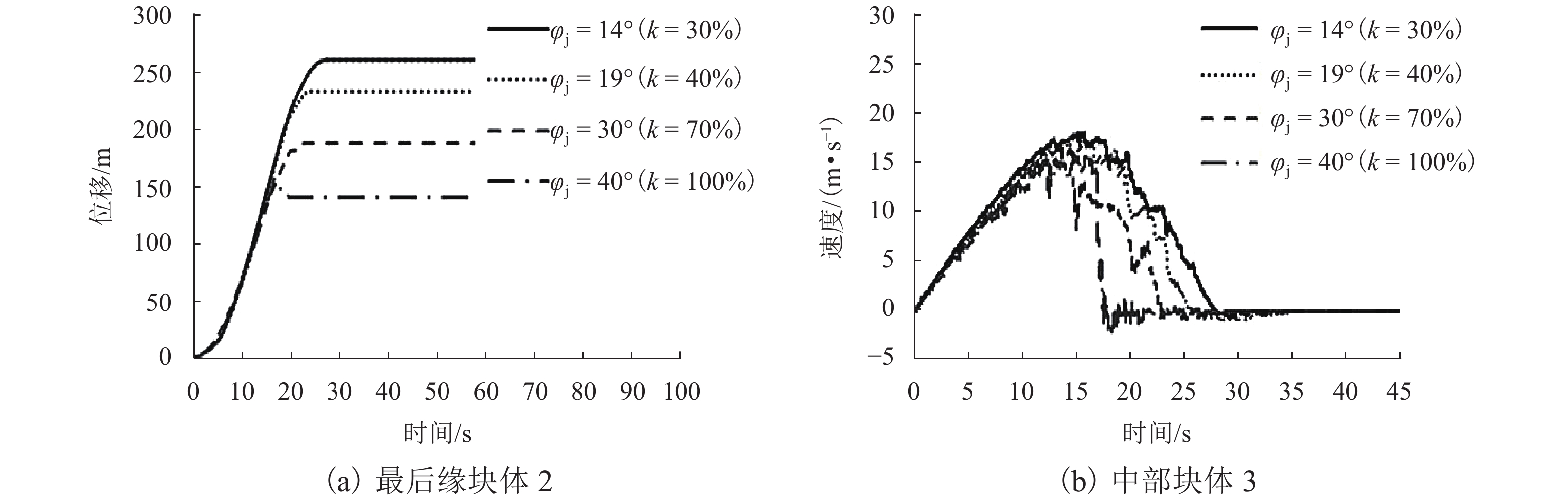
强度衰减是滑坡高速远程运动的重要原因，为了探明滑体强度衰减对滑坡运动能力的影响，以意大利Vajont高速滑坡为例，结合现场调查以及滑坡历史资料，基于岩土体剪切强度衰减理论，利用非连续变形分析（DDA）方法，探讨滑带强度衰减、滑体强度衰减及其共同作用对Vajont滑坡独特运动堆积特征的影响. 研究结果表明：滑带和滑体强度衰减的共同作用造成了Vajont滑坡显著高速运动和独特堆积特征，滑带强度衰减对滑坡运动速度起主导作用，当滑带强度衰减为15.8° 时，监测块体最大速度为5 m/s，当滑带强度衰减为6.9° 时，监测块体的最大速度为19 m/s；滑体强度衰减则对其高速持时具有显著影响，进而大幅提高滑坡运动的远程能力，当滑体强度为40.0° 时，监测块体水平最大位移为140 m，当滑体强度衰减为14.0° 时，监测块体水平最大位移为260 m；数值模拟过程中滑坡呈现出“一体化”运动特征，此特征可用来解释在实际滑坡堆积体高速远程运动过程中保持良好层序的原因.
Abstract:The strength degradation is an important reason for the high-speed and long-distance movement of landslides. In order to explore the influence of landslide strength attenuation on landslide movement ability, taking a high-speed Vajont landslide in Italy as an example, combined with field investigation and landslide history data and based on the shear strength attenuation theory of rock and soil mass, the discontinuous deformation analysis (DDA) method is used to study the influence of sliding band strength attenuation, sliding mass strength attenuation, and their joint action on the unique movement accumulation characteristics of the Vajont landslide. The results show that the remarkable high-speed movement and unique accumulation characteristics of the Vajont landslide are the consequences of strength degradation in both the sliding band and the sliding mass. Among them, the strength attenuation of sliding band play a dominant role in the movement velocity of the landslide. When the strength of sliding band is 15.8° and 6.9°, the maximum velocity of the monitored block is 5 m/s and 19 m/s, respectively. Meanwhile, the strength degradation of sliding mass has a significant effect on its high-speed duration and greatly improves the long-distance ability of landslide movement. When the strength of sliding mass is 40.0° and 14.0°, the maximum horizontal displacement of the monitored block is 140m and 260m, respectively. The ‘en masse’ motion character in the sliding mode can explain well the good strata sequence in the slide deposit after the landslide is fully started.
-
Key words:
- high-speed slide /
- Vajont landslide /
- DDA /
- strength degradation /
- numerical simulation
-
轨道不平顺是加剧轮轨作用力和列车振动的重要诱因. 高速行车条件下，轨道不平顺不仅降低旅客乘坐舒适性，还会加剧轨道结构的疲劳伤损，降低线路使用寿命，甚至造成列车脱轨等安全事故[1]. 因此，保持线路的高平顺性，是高速列车安全平稳运行的重要保障.
我国高速铁路坚持“动态检查为主，动静态检查相结合”的原则. 动态检测以综合检测列车检测结果为主要依据，使用巡检设备、车载式线路检查仪和添乘检查作为辅助手段. 发现问题时，结合现场静态复核，全面分析原因，合理确定维修方案和计划[2]. 诸多轨道不平顺指标中，轨距、水平、三角坑动静态检测原理基本一致，但轨向、高低动静态检测原理却并不相同. 具体来说，轨向、高低动态检测是基于惯性基准的偏差量，而静态检测主要采用中点弦测法和矢距差法得到的偏差值. 在关联性分析方面，杨飞等[3-4]通过车线动力学仿真提出了基于10、20、60 m中点弦测法的轨道不平顺评价方法，并利用5 m中点弦测法评价轨道板周期性不平顺. 相比于动态空间曲线，中点弦测法可以通过改变弦长，更有针对性地评价对行车安全性和舒适性影响显著的轨道不平顺波段. 此外，部分学者还基于中点弦测法和三点偏弦法将平顺性指标逆向还原真实轨道不平顺[5-7]，为评价轨道不平顺提供了新的途径. 相比而言，矢距差法则有一定的局限性，魏晖等[8]推导了中点弦测值转换成矢距差的计算通式，借助矢距差法传递函数可以验证其不适用于高速铁路轨道长波不平顺的静态测量[9-10]. 综上，中点弦测法具备物理意义明确、不存在里程相位差、与车辆动力响应的匹配性更好等诸多优势，更利于进行轨道不平顺动静态关联性分析，指导现场养护维修作业.
目前，对轨道平顺性的静态检查主要依靠轨道测量仪、轨道检查仪或弦线、道尺等设备，受限于天窗时长、测量效率等因素制约，难以实现动静态检查有效结合. 为此，提出基于动态检测数据的动态弦测模型，建立动态不平顺与静态不平顺的映射关系，对于发挥动态检测数据功能，减少静态测量工作量，更好地指导轨道养护维修具有理论价值和现实意义.
1. 动态弦测法原理
轨道动态不平顺是在列车荷载作用下，通过轨道检查车或综合检测列车测得的轨道不平顺. 我国GJ-6型轨道检测系统采用惯性基准法[11]，以高低不平顺检测原理为例，见图1. 车体相对于惯性基准和轴箱的垂向位移分别为Z和W，车轮径为R，车体垂向加速度a经过二次积分，得到车体相对于惯性基准的垂向位移变化量
ΔZ ，用位移计测量车体与轴箱的相对垂向位移变化量ΔW ，轨检系统所在轮对的车轮径跳值ΔR 相对于轨道不平顺可忽略不计，轨道动态高低不平顺F的计算简化为F=ΔZ−ΔW−ΔR≈ΔZ−ΔW = ∬adtdt−ΔW, (1) 式中：t为时间.
对垂向位移变化量
ΔW 和ΔZ 进行高通滤波，剔除无用的长波成分，从而准确测量指定波长范围内的动态高低不平顺. 轨向不平顺的检测原理与之类似.轨道静态不平顺是指在无列车荷载作用下测得的轨道不平顺，其中，静态高低不平顺和轨向不平顺常采用中点弦测正矢或矢距差进行描述[12]. 在轨道静态不平顺容许偏差管理中，高低偏差和轨向偏差为10 m弦测量的正矢值；在轨道静态不平顺长弦测量作业验收中，采用5 m/30 m和150 m/300 m矢距差进行管理；而对于曲线正矢则采用20 m弦测正矢值进行管理[13-14].
动态高低不平顺和轨向不平顺是相对于惯性基准的偏差数据，而静态高低不平顺和轨向不平顺最常用的是中点弦测矢度值，二者在评价结果上存在显著差异[15]. 为建立动态不平顺与静态不平顺的关联关系，将动态高低不平顺和轨向不平顺按中点弦测法输出，从而转换成与静态检测结果一致的弦测值，命名为动态弦测值，记作Q，如图2所示，图中：l为半弦长；vi为第i点的静态高低不平顺；fi为第i点的动态高低或轨向不平顺幅值；
fi−r 和fi+r 分别为第i点所在弦的起点和终点处动态高低或轨向不平顺幅值，r为中点矢距的采样间隔；qi为第i点的中点矢距，如式（2）所示.
图 2 基于动态弦测法的轨道高低不平顺测量Figure 2. Track longitudinal level measurements with the dynamic chord methodqi=fi−fi−r+fi+r2. (2) 对式（2）进行傅里叶变换，得到中点弦测法的幅度谱
|Hq(ω)| 和相位谱φq(ω) 如式（3）所示.{|Hq(ω)|=1−cos(2πl/2πlλλ),φq(ω)=0, (3) 式中：
ω = 2π/λ 为空间角频率，rad/m；λ 为轨道不平顺波长，m.由式（3）可知，中点弦测法的幅值增益与弦长、不平顺波长有关，在0 ~ 2之间波动，相位偏差恒为0，相频无时延和失真[16]. 图3绘制了中点弦测法的幅频特性，将幅值增益不小于1视为有效检测，可以得到10、20、30、40、50、60 m弦对应的有效检测波段分别为7 ~ 20、13 ~ 40、20 ~ 60、27 ~ 80、33 ~ 100、40 ~ 120 m. 动态高低和轨向不平顺原始信号经过数字高通滤波器滤除无用的长波成分，准确截取有效的波长成分，使通带内的幅值增益近似为1[17]. 当弦测法的有效检测波段超出高通滤波截止波长时，低频（长波）成分经高通滤波后衰减，动态弦测值与真实静态弦测值相比会产生较大差异，从而使动态弦测结果长波成分严重失真. 因此，动态弦测法应有最大合理弦长的限制. 我国轨道动态不平顺最大截止波长主要分为42、70、120 m，对于理想滤波器而言，最大截止波长分别42、70、120 m的高通滤波器分别能够覆盖最大弦长为20、30、60 m的有效检测波段. 由于并不存在绝对理想的滤波器，且轨道不平顺是由不同波长、不同幅值和不同相角的简谐波叠加而成的复杂随机波，实际覆盖的最大弦长将会低于这些波段.
2. 动态弦测法特性分析
2.1 动、静态轨道不平顺的差异性分析
根据国外研究经验，可运用单波轨道不平顺分析带通滤波、中点弦测法和偏弦测法对波形扭曲的影响[18]. 同理，为研究动态和静态检测传递特性，可将单波余弦型不平顺作为分析对象. 不平顺波形如图4所示，λ由5 m递增至300 m，波幅A0恒为100 mm. 分别采用截止波长为42、70、120 m的高通滤波器对构造不平顺滤波，模拟得到轨道动态不平顺. 采用弦长为10 ~ 60 m的中点弦，弦长步距10 m，输出构造不平顺的中点弦测值，模拟得到轨道静态不平顺.
图5绘制了波长为5、50、100 m的动态和静态检测波形. 可以看出，单波余弦型不平顺经过高通滤波或中点弦测法处理后，原始波形的形状和幅度都被扭曲，均呈现出中间“下凹”、两侧“上凸”的特征，并且随着截止波长或弦长的增大而增大，影响范围也逐渐向两侧延扩. 中点弦测法具有线性相位特性，“下凹”最低点的所在位置与原始波形的一致. 轨检系统的高通滤波器由于具有良好的相频特性，“下凹”最低点的所在位置也与原始波形相差不大.
图 5 部分典型余弦型不平顺动、静态波形Figure 5. Dynamic and static waveforms of some typical cosine irregularities图6绘制了原始不平顺波幅为100 m的动态和静态不平顺“下凹”峰值随不平顺波长的变化规律. 从动态检测结果来看，同一不平顺波长条件下，高通滤波幅值随着滤波器截止波长的增大而增大. 同一截止波长条件下，动态检测幅值随着不平顺波长的增大而降低，并分别在各自截止波长42、70 m和120 m处存在拐点，超过截止波长后变化趋于平稳，并逐渐降至0. 从静态中点弦测结果来看，同一弦长条件下，当不平顺波长小于等于弦长时，静态弦测值幅值基本保持在原100 mm不变；当不平顺波长超过弦长时，静态弦测值幅值降低，然后逐渐趋于平稳. 当不平顺波长超过各自弦长时，同一不平顺波长条件下，弦长越长，静态弦测值幅值越大.
图 6 动、静态不平顺峰值随波长的变化规律Figure 6. Variation of peak values of dynamic and static irregularity with wavelength从动、静态检测结果对比来看，42 m和70 m滤波幅值分别与10 m和20 m弦测值变化规律基本对应；当不平顺波长大于70 m时，120 m滤波幅值与40 m弦测值变化规律基本对应，这说明动、静态的轨道平顺性评价在一定程度上是等价的. 对于现场常见的单峰型不平顺，当弦长大于不平顺波长时，中点弦测法能够准确测量不平顺的真实幅值，而高通滤波会削弱不平顺幅值测量结果. 考虑到轨道动态不平顺是在有载条件下测得的，更契合列车运营实际情况. 因此，将动态弦测法作为动态检测补充输出方式十分必要.
2.2 动态弦测法检测精度的影响因素
图7绘制了截止波长为42、70 m和120 m动态检测波形经过中点弦测法处理后的动态弦测结果. 相比于高通滤波后的波形，动态弦测波形中间“下凹”、两侧“上凸”的特征变化规律与不平顺波长密切相关，但同样也随着弦长的增大而被放大.
图 7 部分典型余弦型不平顺动态弦对比Figure 7. Comparison of dynamic chords with some typical cosine irregularities图8绘制了动态弦测和静态弦测结果“下凹”峰值随不平顺波长的变化规律. 动态弦测幅值的变化规律与静态弦测相近，呈现出先缓慢降低，后迅速降低并逐渐变缓的趋势，当弦长超过40 m时，不平顺波长与弦长一致时，会存在明显的拐点. 同一弦长条件下，高通滤波截止波长越大，动态弦测幅值越接近真实的静态弦测值. 随着弦长的增大，高通滤波截止波长越小，会使动态弦测幅值与真实的静态弦测值之间的差距越来越大. 为了保证某一弦长的动态弦测精度，必须要求高通滤波的截止波长足够大，也就是说，为了保证某一截止波长的动态弦测精度，必须保证弦长取值应在合理的范围内.
无论是高通滤波、中点弦测还是动态弦测，输出结果的幅值随输入不平顺幅值是线性变化的，因此，其他波幅的变化规律与波幅为100 mm的结果是一致的. 为了进一步定量分析任意固定截止波长条件下弦长的合理取值范围. 计算了不同弦长条件下，真实的静态弦测值与各个截止波长的动态弦测幅值之差占原始不平顺幅值（100 mm）的百分比，可以将其描述为动态弦测法的误差，见表1. 将20%作为误差阈值，误差超过阈值则可认为动态弦测法的精度已经不能达到要求.
表 1 动态弦测误差Table 1. Dynamic chord measurement error% 截止波长/m 弦长/m 10 20 30 40 50 60 42 5.4 20.0 39.3 58.2 73.2 83.6 70 2.4 7.7 16.6 27.5 39.3 51.0 120 2.2 2.7 6.0 10.4 15.7 21.8 由表1得出，截止波长为42、70 m和120 m的动态弦测法最大合理弦长可以分别取为20、30 m和50 m. 考虑到120 m长波不平顺与车辆运行姿态密切相关，测量精度会受到一定影响；但更长波的不平顺幅值往往更大，需要适当降低误差阈值. 因此，将截止波长为120 m的动态弦测法最大合理弦长降为40 m. 在上述各截止波长与合理弦长组合的范围内，同一弦长条件下，动态不平顺截止波长越大，动态弦测法的误差就越小，用最大截止波长为120 m的动态不平顺弦测值来替代静态弦测值的精度更高.
2.3 动态弦测值与原始动态不平顺的关系
计算某高铁线路路基和简支梁区段120 m长波高低不平顺的动态弦测值，弦长取10 ~ 60 m. 统计得到实测高低不平顺峰值和不同弦长动态弦测峰值10% ~ 100%分位数对应的幅值，两者的对应关系如图9所示，图中横轴x为120 m长波高低不平顺的各百分位值，简称“高低不平顺峰值”，纵轴y为动态弦峰值的各百分位值，简称“动态弦峰值”. 同一弦长条件下，动态弦峰值与高低不平顺峰值呈线性关系. 从图9（a）看出：路基区段10 m和20 m动态弦峰值小于高低不平顺峰值，其余弦长均大于高低不平顺峰值；随着弦长的增大，动态弦峰值逐渐增大，且增速越来越慢，30 ~ 60 m动态弦峰值相差不大. 从图9（b）看出：对于简支梁区段，30 m和40 m动态弦峰值最大，这是由于这2个弦在高低不平顺1阶主波长32 m处的幅值增益大于1，主波长32 m的幅值被充分放大；而10 m和60 m动态弦峰值小于原始值，因为60 m弦在32 m处的幅值增益小于1，导致60 m动态弦峰值偏小. 综上所述，动态弦峰值与高低不平顺峰值的各百分位值呈线性关系，但由于路基和简支梁区段不同波长的动态幅值分布规律大不相同，因此，拟合系数在两种基础结构的检测结果存在较大差异.
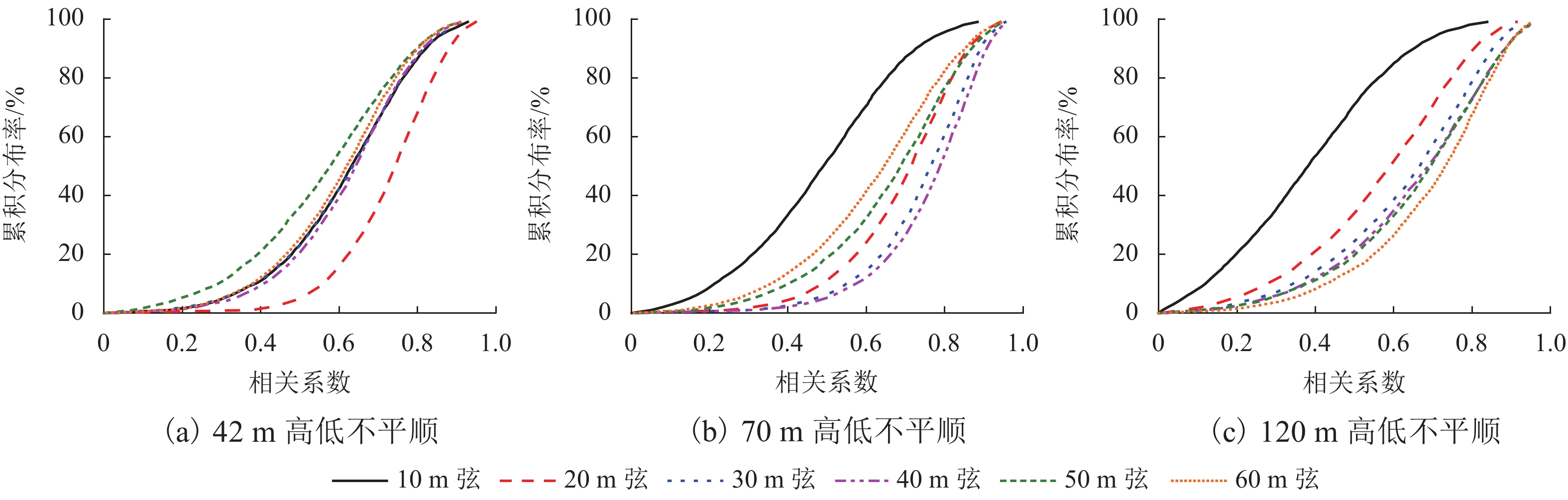
图 9 动态弦与原始动态高低不平顺峰值的关系Figure 9. Relationship between dynamic chord and original dynamic longitudinal level peak基于某高速铁路全线动态检测数据，每200 m作为1个计算单元，逐个计算动态弦测值与动态原始值的相关系数，并作累计分布如图10所示. 可以看出：不同截止波长的相关系数分布规律不同；截止波长为42 m的高低不平顺，20 m动态弦测波形与其相关性最优，50 m动态弦测波形与其相关性最差；截止波长为70 m的高低不平顺，30 m和40 m动态弦测波形与其相关性最优，10 m动态弦测波形与其相关性最差；截止波长为120 m的高低不平顺，30 ~ 60 m动态弦测波形与其相关性比较接近，10 m动态弦测波形与其相关性最差.
图 10 动态弦与实测动态高低不平顺相关性Figure 10. Correlation between dynamic chord and measured dynamic longitudinal level3. 动态弦测法验证及其应用
3.1 路基沉降区段检算
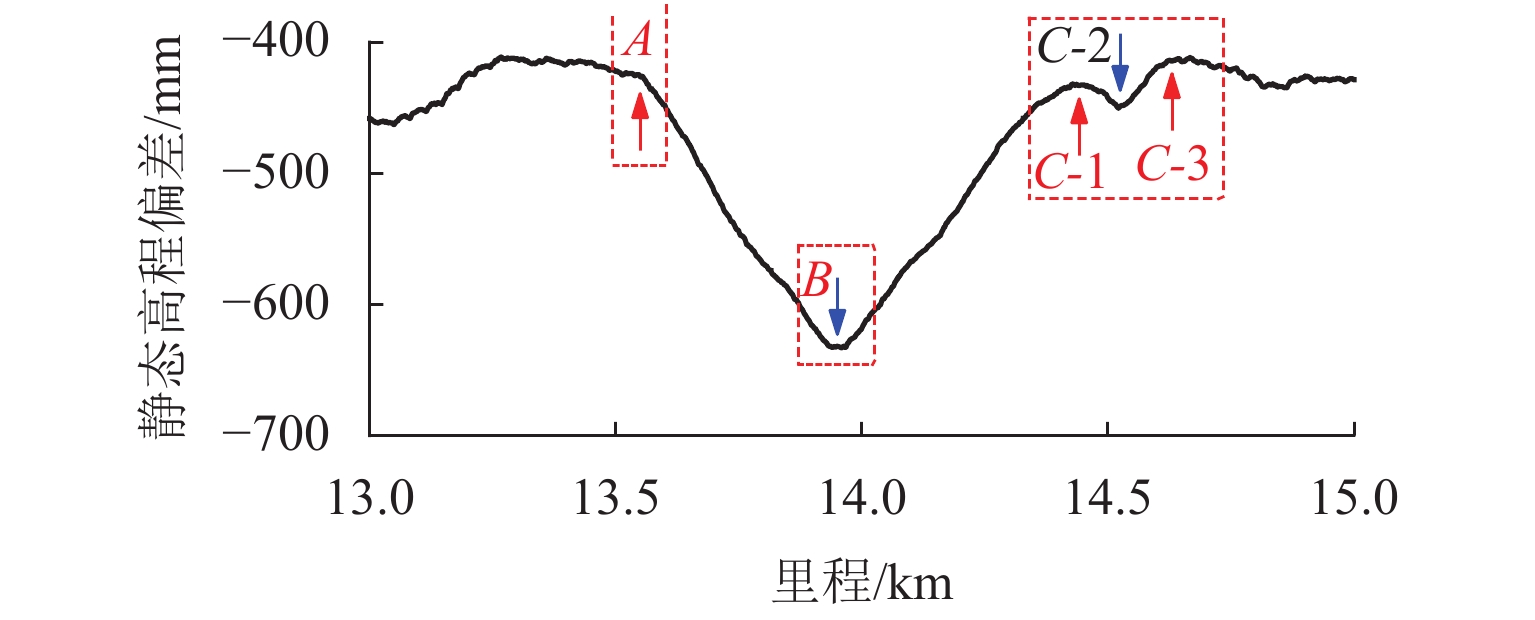
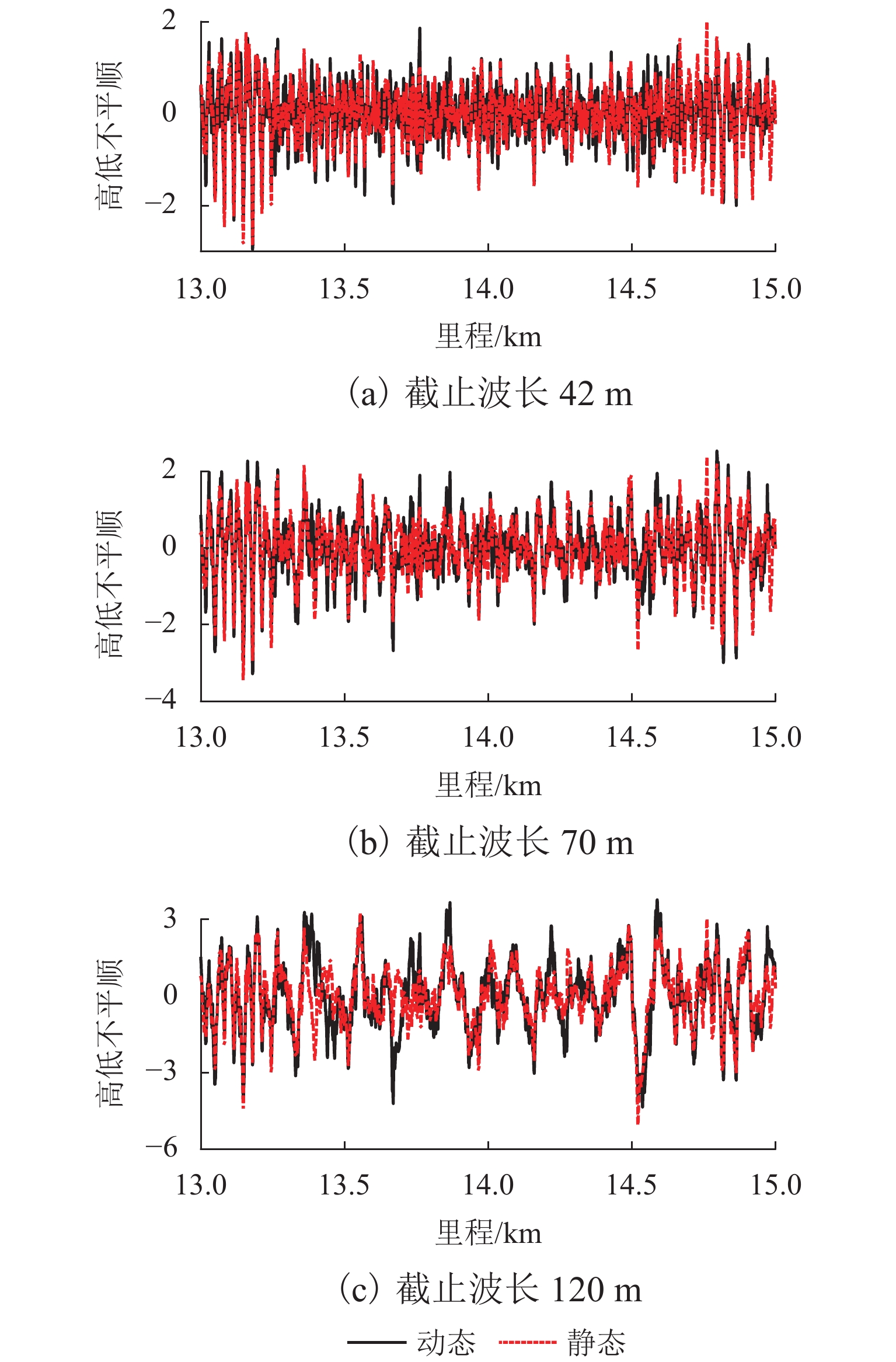
以某高铁线路路基区段检测数据为例，静态高程偏差如图11所示，图中，区段A为沉降起始点，B为沉降点，区段C中，C-2处为沉降点，C-1和C-3处则为两侧的沉降区段起终点. 实际线位与设计线位的最小高程偏差为 −413 mm，最大高程偏差达到 −633 mm，该区段整体沉降较为显著. 分别采用轨检系统截止波长为42、70 m和120 m高通滤波器对静态高程偏差进行滤波，与动态高低不平顺的对比如图12所示. 可以看出：3种截止波长条件下，动、静态数据均吻合很好，验证了该区段动静态检测数据的有效性.
分别将该区段截止波长为42、70 m和120 m的实测动态高低不平顺，按10 ~ 60 m动态弦重新输出. 同时，将实测静态高程偏差同样按10 ~ 60 m中点弦测输出，计算静态高程偏差的弦测值. 各个弦长对应动、静态弦测值如图13所示. 可以看出：当弦长为最短的10 m时，静态高程偏差弦测值与截止波长为42、70 m和120 m动态弦测的波形重合性均非常好. 说明这3种截止波长的动态高低不平顺按10 m弦测重新输出后，均可以准确表达静态的10 m弦测值. 但随着弦长的增大，静态弦测值的长波成分逐渐显现出来，动态弦测值与静态弦测值间在其中3个区段的差距越来越大，分别位于K13 + 500—K13 + 600、K13 + 900—K14 + 000和K14 + 400—K14 + 600，其余区段动静态重合性依旧很好. 从图13中还可以看出：对于上述3个区段，在同一弦长条件下，动态高低不平顺的截止波长越短，它所包含的长波成分就越少，因此，其动态弦测值与静态弦测值间的差距也越大.
图 13 路基区段动态弦测与静态弦测对比Figure 13. Comparison between dynamic and static chord measurements in subgrade section上述3个差异较大区段动、静态弦测值的峰值差如表2所示. 参考《铁路基础设施动态检测——轨道几何检测系统（Q/CR 751—2020）》[19]对中高速轨道几何检测系统检测技术指标的规定，截止波长为42、70、120 m对应的最大允许误差分别为 ±1、±2、±3 mm. 利用该标准评价动态弦测值是否满足精度要求. 截止波长为42 m时，当弦长为20 m时仅有1处超限，弦长大于20 m时3处均超限，因此，最大合理弦长可取为20 m. 截止波长为70 m时，当弦长小于等于30 m时均未超限，弦长大于30 m时均超限，因此，最大合理弦长可取为30 m. 截止波长为120 m时，当弦长小于等于40 m时均未超限，弦长大于40 m时有2处超限，因此，最大合理弦长可取为40 m. 该结论均与2.2节中得到最大合理弦长一致，验证了最大弦长的合理性.
表 2 动态弦测值与静态弦测值峰值差Table 2. Peak value difference between dynamic chord measurement and static chord measurement mm弦长/m 截止波长/m 动、静态弦测值峰值差 A B C-1 C-2 C-3 10 42 0.2 0.3 0.1 0.4 0.1 70 0.2 0.2 0.1 0.3 0.1 120 0.1 0.2 0.1 0.2 0.1 20 42 0.8 0.8 0.4 1.3 0.6 70 0.6 0.7 0.4 0.9 0.5 120 0.4 0.6 0.3 0.6 0.3 30 42 1.7 1.5 0.5 2.7 1.3 70 1.2 1.4 0.4 1.9 0.9 120 0.8 1.2 0.3 1.2 0.6 40 42 2.8 2.7 1.4 4.5 0.9 70 2.1 2.6 1.4 3.3 0.7 120 1.4 2.2 1.2 2.2 0.5 50 42 4.0 4.1 2.0 6.4 3.0 70 3.1 4 1.9 4.8 2.6 120 2.0 3.4 1.7 3.2 1.8 60 42 5.2 5.6 2.9 7.7 4.0 70 4.3 5.6 2.7 6.1 3.6 120 2.9 4.8 2.4 4.0 2.5 尽管弦长超过最大合理弦长时，动态弦测法的精度已经不能达到要求，但仍有实用价值. 可在缺少静态绝对测量数据的条件下，结合动态弦测数据和轨检仪的静态弦测数据识别沉降区段. 对照图13（f），C-1和C-3处静态弦测值明显朝正方向偏离动态弦测值，C-2处明显朝负方向偏离动态弦测值. C处上述动静态弦测值之差的变化趋势与该处高程偏差变化趋势特征一致. 对比区段A、B和C可知，A处静态弦测值明显朝正方向偏离动态弦测值，B处明显朝负方向偏离动态弦测值，C处整体要朝正方向偏离动态弦测值. 并随着弦长的增大偏离越大，弦长达到60 m时最显著. 对照图11发现，A、B和C处整体的高程偏差变化趋势同样与上述特征一致，说明B处是沉降点，A和C-1处是两侧的沉降区段起终点. 综上，静态弦测值明显朝负方向偏离动态弦测值的处所为沉降点，相邻两侧朝正方向偏离动态弦测值的处所为沉降区段起终点.
3.2 简支梁区段检算
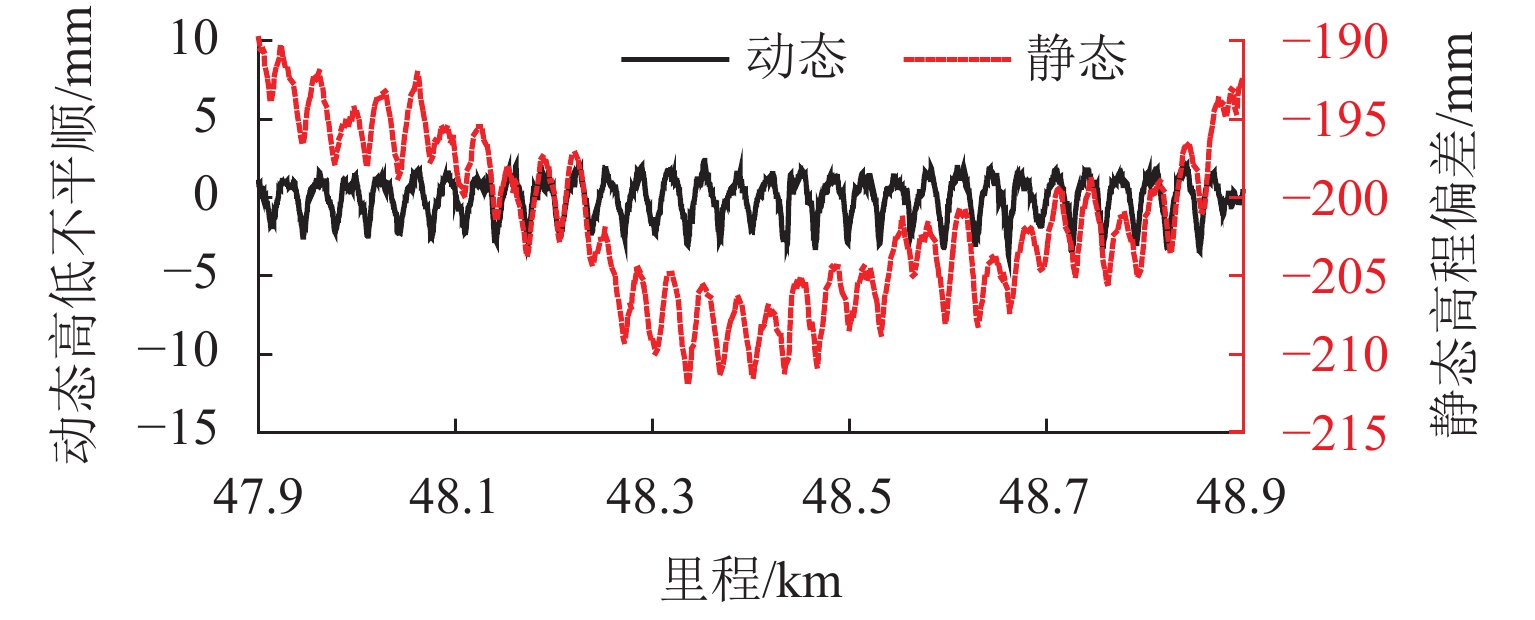
以某高铁线路简支梁区段检测数据为例，动、静检数据对比如图14所示，截止波长为42 m的高低不平顺峰值达到 −3.7 mm，静态高程偏差最小达到−190 mm，最大达到 −212 mm.
图15绘制了该区段动态弦测值与静态高程偏差的弦测值的对比. 弦长由10 m增至60 m，动态弦测值与静态弦测值间波形和幅值的差异越来越大，动、静态弦测值之差的95%分位数分别为0.9、1.4、2.0、2.1、2.2、2.3 mm. 可见对于截止波长为42 m的动态高低不平顺，当弦长增至20 m时，动、静态弦测值之差95%分位数满足小于2 mm要求. 因此，同样可以验证截止波长为42 m的动态弦测法最大合理弦长取20 m.
图 15 简支梁区段动态弦测与静态弦测对比Figure 15. Comparison between dynamic and static chord measurements in simply supported beam section4. 结 论
1） 由于动态高低和轨向不平顺是相对于惯性基准的偏差数据，而静态高低和轨向不平顺最常用的是中点弦测矢度值，导致二者在结果上存在显著差异. 此外，动态是在有载情况下进行检测，比静态检查贴合实际运行，为避免对现场维修造成困扰，采用动态弦测方法将动态高低和轨向不平顺转换为动态弦测值十分必要.
2） 由动静态检测结果对比得出，42 m和70 m动态高通滤波幅值分别与10 m弦和20 m弦测值变化规律基本对应. 当不平顺波长大于70 m时，120 m动态高通滤波幅值与40 m弦测值变化规律基本对应.
3） 动态弦测值与原始动态不平顺的各百分位值统计上呈线性关系，但不同区段拟合系数存在较大差异；截止波长为42、70、120 m的原始动态不平顺，分别与弦长为20、30 ~ 40、30 ~ 60 m的动态弦测波形相关性最优.
4） 动态检测的截止波长包括42、70、120 m，对应的动态弦测法最大合理弦长分别取为20、30、40 m，通过路基和简支梁区段实测数据验证了动态弦测法的合理性.
5） 基于沉降区段实测数据分析得出，弦长为60 m时，静态弦测值明显朝负方向偏离动态弦测值的处所为沉降点，相邻两侧朝正方向偏离动态弦测值的处所为沉降区段起终点，这可以用于沉降区识别和监控.
致谢：中国铁道科学研究院集团有限公司科技研究开发计划（2020YJ048）项目支持.
-
图 2 Vajont峡谷两岸地层状况
Figure 2. Stratigraphic conditions on both sides of the Vajont Valley
图 3 更新的Vajont峡谷两岸的地层序列（单位：m）
Figure 3. Updated lithostratigraphic columns on both sides of the Vajont Valley (unit: m)
图 5 滑坡堆积体及“飞来峰”的层序保持良好
Figure 5. Well-preserved strata sequence of klippe and slide deposit
图 8 不同内摩擦角时最前缘块体 1 的位移时间曲线
Figure 8. Displacement-time history of the leading edge block 1 with different friction angles
图 9 φs = 21.0°，Vajont 斜坡模型最终的状态
Figure 9. Ultimate state of the Vajont slope model with φs = 21.0°
图 10 φs衰减至不同值时DDA模拟滑坡的运动全过程（φj = 30.0°）
Figure 10. Whole process of landslide motion by DDA simulation withthe sliding band strength φs decaying to different values（φj = 30.0°）
图 11 φs（滑带强度）衰减至不同值时监测块体的位移及速度时程曲线（φj = 30.0°）
Figure 11. Time histories of velocity and displacement for monitored blocks with the sliding band strength φs decaying to different values (φj = 30.0°)
图 12 不同φj时滑坡最终堆积形态（φs = 9.2°）
Figure 12. Ultimate deposit outline of models with the sliding mass strength φj decaying to different values (φs = 9.2°)
图 13 φj（滑体强度）衰减至不同值时，监测块体的位移时程曲线（φs = 9.2°）
Figure 13. Displacement-time history of monitored blocks with the strength of slide mass φj decaying to different values (φs = 9.2°)
表 1 Vajont滑坡的物理参数
Table 1. Physical parameters of the Vajont landslide
项目 密度 ρ/
（ kg•m−3）重度 wy/
（ kN•m−3）杨氏模量 E/
GPa泊松比 μ 基岩 2 700 26.46 19 0.35 滑体 2 700 26.46 15 0.31 
下载: 导出CSV
表 2 节理参数
Table 2. Joint parameters
位置 黏聚力
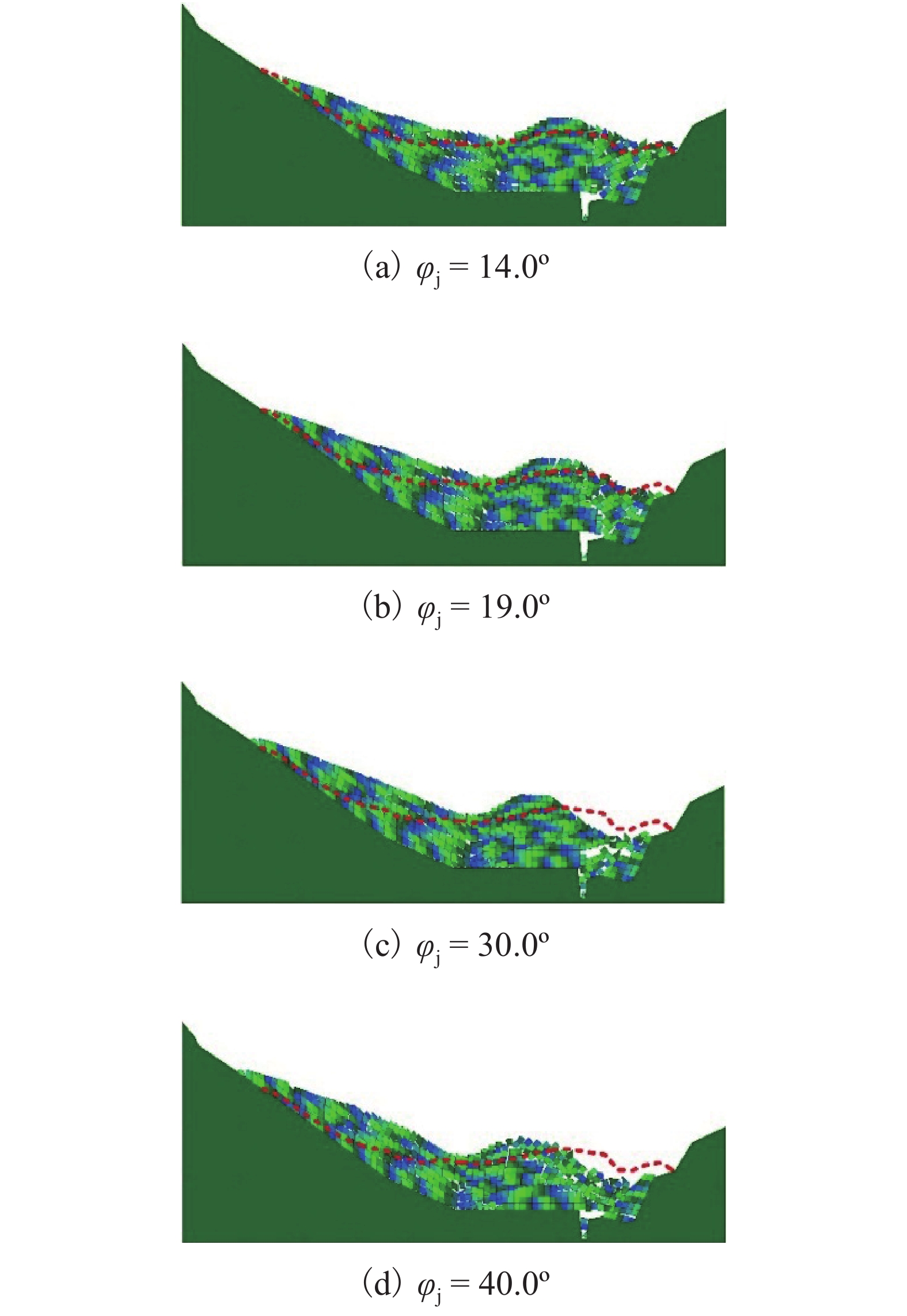
c /MPa内摩擦角
φj /（°）抗拉强度/Pa 岩体内部节理 2.5 40（稳定时）
30（破坏后）0
下载: 导出CSV
表 3 模型控制参数
Table 3. Model control parameters
项目 数值 动力系数 1.0 单步允许最大位移率 0.001 时间步/s 0.005 弹簧刚度/（ × 1011 N•mm−1） 1 超松弛系数 1.3
下载: 导出CSV
表 4 滑带内摩擦角不同时滑坡的最大速度
Table 4. Maximum velocities of the landslide with different friction angles of sliding band
φs/（°） 最大速度/（m•s−1） 6.9 19.47 9.2 16.74 11.4 13.60 15.8 5.05
下载: 导出CSV
-
[1] MÜLLER-SALZBURG L. The rock slide in the Vajont valley[M]. Springer-Verlag, 1964: 148-212. [2] MÜLLER-SALZBURG L. The Vajont catastrophe-A personal review[J]. Engineering Geology, 1987, 24(1/2/3/4): 423-444. [3] HENDRON A J, PATTON F D. The Vaiont slide: a geotechnical analysis based on new geological observations of the failure surface: US army engineer waterways experiment station[R]. Washington D. C.: Department of the Army US Army Corps of Engineers, 1985. [4] SUPERCHI L, FLORIS M, GHIROTTI M, et al. Implementation of a geodatabase of published and unpublished data on the catastrophic Vaiont landslide[J]. Natural Hazards and Earth System Sciences, 2010, 10(4): 865-873. [5] ALONSO E E, PINYOL N M. Criteria for rapid sliding I: a review of Vaiont case[J]. Engineering Geology, 2010, 114(3/4): 198-210. [6] PARONUZZI P, BOLLA A. The prehistoric Vajont rockslide:an updated geological model[J]. Geomorphology, 2012, 169(10): 165-191. [7] CECINATO F, ZERVOS A, VEVEAKIS E. A thermo-mechanical model for the catastrophic collapse of large landslides[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2010, 35(14): 1507-1535. [8] HABIB P. Production of gaseous pore pressure during rock slides[J]. Rock Mechanics and Rock Engineering, 1975, 7(4): 193-197. [9] NONVEILLER E. The Vajont reservoir slope failure[J]. Engineering Geology, 1987, 24(87): 493-512. [10] VOIGHT B, FAUST C. Frictional heat and strength loss in some rapid landslides[J]. Geotechnique, 1982, 32(1): 43-54. doi: 10.1680/geot.1982.32.1.43 [11] ARDOULAKIS I. Dynamic thermo-poro-mechanical analysis of catastrophic landslides[J]. Geotechnique, 2002, 52(3): 157-171. [12] PINYOL N M, ALONSO E E. Criteria for rapid sliding Ⅱ.: thermo-hydro-mechanical and scale effects in Vaiont case[J]. Engineering Geology, 2010, 114(3/4): 211-227. [13] HU W, HUANG R Q, MCSAVENEY M, et al. Superheated steam,hot CO2 and dynamic recrystallization from frictional heat jointly lubricated a giant landslide:field and experimental evidence[J]. Earth and Planetary Science Letters, 2019, 510: 85-93. doi: 10.1016/j.jpgl.2019.01.005 [14] TIKA T E, HUTCHINSON J N. Ring shear tests on soil from the Vaiont landslide slip surface[J]. Geotechnique, 1999, 49(1): 59-74. doi: 10.1680/geot.1999.49.1.59 [15] FERRI F, DI TORO G, HIROSE T, et al. Low-to high-velocity frictional properties of the clay-rich gouges from the slipping zone of the 1963 Vaiont slide,northern Italy[J]. Journal of Geophysical Research:Solid Earth, 2011, 116(B9): 1-17. [16] 崔圣华,裴向军,黄润秋,等. 大光包滑坡不连续地质特征及其工程地质意义[J]. 西南交通大学学报,2019,54(1): 65-76.CUI Shenghua, PEI Xiangjun, HUANG Runqiu, et al. Discontinuities and engineering geological significances of strong earthquake-induced daguangbao landslide[J]. Journal of Southwest Jiaotong University, 2019, 54(1): 65-76. [17] ZHANG Y B, CHEN G Q, ZHANG L, et al. Effects of near-fault seismic loadings on run-out of large-scale landslide:a case study[J]. Engineering Geology, 2013, 166(11): 216-236. [18] ZHANG Y B, WANG J M, XU Q, et al. DDA validation of the mobility of earthquake-induced landslides[J]. Engineering Geology, 2015, 194: 38-51. doi: 10.1016/j.enggeo.2014.08.024 [19] ZHANG Y B, XU Q, CHEN G Q, et al. Extension of discontinuous deformation analysis and application in cohesive-frictional slope analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 70(10): 533-545. [20] 邬爱清,丁秀丽,李会中,等. 非连续变形分析方法模拟千将坪滑坡启动与滑坡全过程[J]. 岩石力学与工程学报,2006,25(7): 1297-1303. doi: 10.3321/j.issn:1000-6915.2006.07.001WU Aiqing, DING Xiuli, LI Huizhong, et al. Numerical simulation of startup and whole failure process of Qianjiangping landslide using discontinuous deformation analysis method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1297-1303. doi: 10.3321/j.issn:1000-6915.2006.07.001 [21] 赵兴权,张迎宾,陈光齐,等. 非连续变形分析方法及其在灾害防治研究中的应用[J]. 西南交通大学学报,2016,51(2): 300-312. doi: 10.3969/j.issn.0258-2724.2016.02.010ZHAO Xingquan, ZHANG Yingbin, CHEN Guangqi, et al. Discontinuous deformation analysis method and its applications to disaster prevention[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 300-312. doi: 10.3969/j.issn.0258-2724.2016.02.010 [22] 刘军,李仲奎. 非连续变形分析(DDA)方法研究现状及发展趋势[J]. 岩石力学与工程学报,2004,23(5): 839-845. doi: 10.3321/j.issn:1000-6915.2004.05.024LIU Jun, LI Zhongkui. Current situation and development of DDA method[J]. Journal of Southwest Jiaotong University, 2004, 23(5): 839-845. doi: 10.3321/j.issn:1000-6915.2004.05.024 [23] 姜清辉,周创兵. 岩土工程不连续变形分析计算中的若干问题[J]. 岩石力学与工程学报,2007,26(10): 2014-2026. doi: 10.3321/j.issn:1000-6915.2007.10.009JIANG Qinghui, ZHOU Chuangbing. Some issues in discontinuous deformation analysis for geotechnical engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2014-2026. doi: 10.3321/j.issn:1000-6915.2007.10.009 [24] 陈岩岩. Vajont滑坡稳定性及高速运动特征的DDA模拟研究[D]. 成都: 西南交通大学, 2017. [25] SEMENZA E. Sintesi degli studi geologici sulla frana del Vajont dal 1959 al 1964[J]. Museo Tridentino di Scienze Naturali, 1965, 16: 1-52. [26] SEMENZA E, GHIROTTI M. History of the 1963 Vaiont slide:the importance of geological factors[J]. Bulletin of Engineering Geology and the Environment, 2000, 59(2): 87-97. [27] 张迎宾,余鹏程,赵兴权. 类梯形山体的地震动力响应分析[J]. 西南交通大学学报,2015,50(3): 435-441. doi: 10.3969/j.issn.0258-2724.2015.03.008ZHANG Yingbin, YU Pengcheng, ZHAO Xingquan. Analytical solutions of earthquake dynamic responses of trapezoid-like mountain[J]. Journal of Southwest Jiaotong University, 2015, 50(3): 435-441. doi: 10.3969/j.issn.0258-2724.2015.03.008 [28] TROLLOPE D H. The Vajont slope failure[J]. Rock Mechanics and Rock Engineering, 1980, 13(2): 71-88. [29] BOON C W, HOULSBY G T, UTILI S. New insights into the 1963 Vajont slide using 2D and 3D distinct-element method analyses[J]. Geotechnique, 2014, 64(10): 800-816. doi: 10.1680/geot.14.P.041 [30] SUPERCHI L. The Vajont rockslide: new techniques and traditional methods to re-evaluate the catastrophic event[D]. Padova: Padova University, 2012. [31] 郑颖人,赵尚毅,孔位学,等. 极限分析有限元法讲座——I岩土工程极限分析有限元法[J]. 岩土力学,2005,26(1): 163-168. doi: 10.3969/j.issn.1000-7598.2005.01.035ZHENG Yingren, ZHAO Shangyi, KONG Weixue, et al. Geotechnical engineering limit analysis using finite element method[J]. Rock and Soil Mechanics, 2005, 26(1): 163-168. doi: 10.3969/j.issn.1000-7598.2005.01.035 [32] 郑颖人,赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报,2004,23(19): 3381-3388. doi: 10.3321/j.issn:1000-6915.2004.19.029ZHENG Yingren, ZHAO Shangyi. Application of strength reduction fem in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381-3388. doi: 10.3321/j.issn:1000-6915.2004.19.029 [33] MACLAUGHLIN M M. Discontinuous deformation analysis of the kinematics of landslides[D]. Berkeley: University of California, 1997. [34] MACLAUGHLIN M, SITAR N, DOOLIN D, et al. Investigation of slope-stability kinematics using discontinuous deformation analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(5): 753-762. [35] GHIROTTI M. Edoardo semenza: the importance of geological and geomorphological factors in the identification of the ancient Vaiont landslide[M]. Netherlands: Springer, 2006: 395-406. [36] BARTON N. The shear strength of rock and rock joints[J]. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 1976, 13(9): 255-279. 期刊类型引用(3)
1. 张永亮，朱光增，刘沛. 考虑高阶振型效应的大跨度钢桁拱桥瑞利阻尼参数取值研究. 桥梁建设. 2024(04): 14-20 . 
百度学术2. 孔祥敏，郭光旭，李帅，张蕾. 近场脉冲型地震动下高墩大跨连续刚构拱组合桥地震响应分析. 科技与创新. 2024(23): 102-104 . 百度学术3. 崔叔岩，余瑞峰，陈小平，黄骏，杨华平. 设置摩擦摆支座的大跨径宽幅连续钢箱梁桥抗震性能研究. 成都大学学报(自然科学版). 2024(04): 424-429 . 百度学术其他类型引用(1)
-
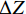
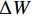
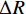
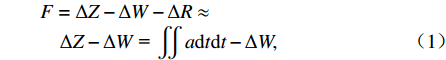
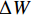
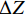
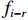
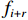
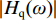
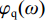
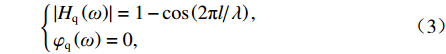
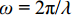
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 673
- HTML全文浏览量: 349
- PDF下载量: 29
- 被引次数: 4