Steel Corrosion Monitoring Based on Partial Modulus of Magnetic Gradient Tensor
-
摘要:
为研究钢筋混凝土中钢筋锈蚀的无损及定量监测方法,分析地球背景磁场和环境干扰磁场的影响,探讨钢筋的锈蚀率与磁场梯度张量局部模量的理论公式. 通过8根钢筋进行通电加速锈蚀试验模拟钢筋不同程度的锈蚀. 研制钢筋锈蚀监测系统,测量锈蚀前后钢筋的磁感应强度,采用磁场梯度张量局部模量反演钢筋的锈蚀率. 试验结果表明:在钢筋锈蚀后测试的磁感应强度曲线发生非等距离的偏移,磁感应强度绝对值相比锈蚀前有增大也有降低,没有一致性的规律;在锈蚀后钢筋磁场梯度绝对值及局部模量的平均值减小;在钢筋锈蚀的磁场监测中,钢筋自身的磁场梯度及局部模量远远大于环境磁场,环境磁场的梯度及其局部模量可忽略不计;8根试件的计算锈蚀率与试验中实际失重率的最小误差为0.22%,最大误差为9.40%,误差的平均值为3.92%,误差的标准差为3.32%.
Abstract:In order to find a nondestructive and quantitative monitoring method for steel corrosion in reinforced concrete, theoretical formulas of the partial modulus and corrosion rate of rebar are derived with consideration of the influence of the Earth’s background magnetic field and environmental interference magnetic field. Accelerated corrosion tests were performed on 8 steel bars through electrification to obtain specimens with different degrees of corrosion. A rebar corrosion monitoring system was then developed to measure the magnetic field intensity of rebar before and after corrosion. Finally, the partial modulus of the magnetic gradient tensor is used to calculate the corrosion rate of the rebar. Results show that the magnetic field intensity curve of the rebar is generally shifted after corrosion, but the absolute value after corrosion may increase or decrease compared with that before corrosion, without consistency. The absolute value of the magnetic gradient and the average value of the partial modulus of the steel bar after corrosion are less than their counterparts before corrosion. In the magnetic monitoring of rebar corrosion, the magnetic gradient and partial modulus of the rebar are much larger than those of the environmental magnetic field, and therefore the gradient of the environmental magnetic field and its partial modulus are negligible. The minimum error between calculated and measured corrosion rates of the 8 specimens is 0.22%, while the maximum error is 9.40%, and the average error is 3.92%, with a standard deviation of 3.32%.
-
Key words:
- reinforced concrete /
- rebar /
- corrosion monitoring /
- magnetic gradient /
- partial modulus
-
钢筋锈蚀会减少钢筋横截面面积,降低钢筋混凝土构件的承载力、引起裂缝开展并反过来加剧锈蚀发展,从而减少结构的耐久性及使用寿命[1],有必要对既有钢筋混凝土结构在服役过程中钢筋锈蚀损伤进行监测,保障钢筋混凝土结构的安全. 磁记忆检测作为一种被动式、非接触式的磁场检测方法[2-6],可得到应力集中或几何形体不连续的区域. 不同于需要施加外部磁场的漏磁检测[4],磁记忆检测通过测量铁磁构件在外部荷载或者地球磁场及环境干扰磁场作用下的微弱磁场. 磁记忆检测通常包括2个重要的磁场参数:垂直于铁磁构件表面的法向磁感应强度及平行于铁磁构件表面的切向磁感应强度. 通常测得的磁感应强度包含铁磁构件自身的磁感应强度和环境磁场[7-9],其中环境磁场包括地球背景磁场及环境干扰磁场,而地球背景磁场及环境干扰磁场并不恒定,从总磁感应强度中分离地球背景磁场及环境干扰磁场非常困难,无法精确测得铁磁构件自身的磁感应强度,因此,采用磁感应强度的磁记忆锈蚀监测方法目前仅可定性评价铁磁构件的锈蚀,在定量监测方面存在困难.
磁场梯度张量可反映磁源体(或铁磁构件)的磁矩信息,受地磁背景磁场及环境干扰磁场的影响较小[10]. 另外,磁源体的磁矩与磁源体的体积、几何形状、边界条件及磁化强度直接相关[10-12],因此,磁矩可反映铁磁性构件的锈蚀. 磁场梯度张量的模量由9个磁场梯度参数计算得到,是磁源体的磁矩及磁源体至测点的距离的函数,可反映铁磁构件的磁矩及几何边界. 但在很多情况下仅可测得部分磁场梯度参量[13-14]. 将这些部分磁场梯度参数充分利用,并延伸应用在锈蚀损伤监测,具有重要的科学意义和工程意义.
对于磁记忆在钢筋锈蚀定量及无损监测方面尚需要进一步研究,分析环境磁场的影响,探讨磁场梯度张量局部模量与钢筋锈蚀率之间的关系,提出相应的理论公式. 采用8根钢筋进行通电加速锈蚀试验模拟钢筋不同程度的锈蚀,然后测量锈蚀前后钢筋的磁感应强度,分析环境磁场对测试的影响,探讨钢筋锈蚀前后的磁感应强度、磁场梯度及相应的局部模量的规律,分析验证磁场梯度局部模量与钢筋锈蚀率的理论公式的准确性.
1. 基于磁场梯度张量局部模量的钢筋锈蚀监测理论
对钢筋锈蚀进行磁场监测时,实际得到的磁感应强度为
{{\boldsymbol{B}}_{\rm{T}}} = {\boldsymbol{B}} + {{\boldsymbol{B}}_{\rm{S}}} = {\boldsymbol{B}} + {{\boldsymbol{B}}_{\rm{E}}} + {{\boldsymbol{B}}_{\rm{N}}}, (1) 式中:{\boldsymbol{B}}为钢筋自身的磁感应强度;{{\boldsymbol{B}}_{\rm{S}}}为环境磁场的磁感应强度;{{\boldsymbol{B}}_{\rm{E}}}为地球背景磁场的磁感应强度;{{\boldsymbol{B}}_{\rm{N}}}为环境干扰磁场的磁感应强度.
同样,实际测量的磁场梯度为
{{\boldsymbol{G}}_{\rm{T}}} = {\boldsymbol{G}} + {{\boldsymbol{G}}_{\rm{S}}}{ = {\boldsymbol{G}}} + {{\boldsymbol{G}}_{\rm{E}}} + {{\boldsymbol{G}}_{\rm{N}}}, (2) 式中:{\boldsymbol{G}}为钢筋自身的磁场梯度;{{\boldsymbol{G}}_{\rm{S}}}为环境磁场的梯度;{{\boldsymbol{G}}_{\rm{E}}}为地球背景磁场的梯度;{{\boldsymbol{G}}_{\rm{N}}}为环境干扰磁场的梯度.
钢筋自身的磁感应强度{\boldsymbol{B}}根据测试距离在几百nT至几万nT,{{\boldsymbol{B}}_{\rm{E}}}大约50 000 nT[15-17],环境干扰磁场的大小取决于环境干扰磁场的来源. 从总磁感应强度中消除过滤地球背景磁场和环境干扰境磁场而得到钢筋自身的磁感应强度,目前存在较大的困难[16-17]. 同时,地球背景磁场的垂向梯度约20 × 10−6 nT/mm,水平梯度约5 × 10−6 nT/mm[15-17],远远小于钢筋自身的磁场梯度值,即{\boldsymbol{G}} \gg {{\boldsymbol{G}}_{\rm{E}}},同时在测试中尽量远离或消除环境干扰磁场,因此可认为磁场梯度张量{{\boldsymbol{G}}_{\rm{T}}}仅由钢筋产生,式(2)转化为
{{\boldsymbol{G}}_{\rm{T}}} = {\boldsymbol{G}} + {{\boldsymbol{G}}_{\rm{S}}} = {\boldsymbol{G}} + {{\boldsymbol{G}}_{\rm{E}}} + {{\boldsymbol{G}}_{\rm{N}}} \approx {\boldsymbol{G}}. (3) 如钢筋自身的磁感应强度{\boldsymbol{B}}表示为{B_x}、{B_y}和{B_{\textit{z}}}. 则G可表示为
{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {B_x}}}{{\partial x}}}&{\dfrac{{\partial {B_x}}}{{\partial y}}}&{\dfrac{{\partial {B_x}}}{{\partial {\textit{z}}}}} \\ {\dfrac{{\partial {B_y}}}{{\partial x}}}&{\dfrac{{\partial {B_y}}}{{\partial y}}}&{\dfrac{{\partial {B_y}}}{{\partial {\textit{z}}}}} \\ {\dfrac{{\partial {B_{\textit{z}}}}}{{\partial x}}}&{\dfrac{{\partial {B_{\textit{z}}}}}{{\partial y}}}&{\dfrac{{\partial {B_{\textit{z}}}}}{{\partial {\textit{z}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{B_{{xx}}}}&{{B_{{xy}}}}&{{B_{{x{\textit{z}}}}}} \\ {{B_{{yx}}}}&{{B_{{yy}}}}&{{B_{{y{\textit{z}}}}}} \\ {{B_{{{\textit{z}}x}}}}&{{B_{{{\textit{z}}y}}}}&{{B_{{{\textit{z}}{\textit{z}}}}}} \end{array}} \right]. (4) 根据麦克斯韦方程组,磁场梯度G对称且其迹为0[11-12]. 则磁场梯度张量中,仅含有5个独立的参量,即{B_{{xx}}}、{B_{{xy}}}、{B_{{x{\textit{z}}}}}、{B_{{y{\textit{z}}}}}、{B_{{yy}}}.
磁场梯度张量的模量为
C = \sqrt{ {\sum {{{\boldsymbol{B}}^2_{ij}}} } }, (5) 式中:i和j为x、y和z.
将磁场梯度张量中的9个梯度参量缩并为1个标量,即模量C,称为磁场梯度张量的全局缩并.
定义磁场梯度张量的局部模量{C_{\rm{n}}}[14]为
{C_{\rm{n}}} = \left\{ {\begin{array}{*{20}{l}} {\sqrt {B_{{xx}}^2 + B_{{yx}}^2 + B_{{{\textit{z}}x}}^2} }\;,\\ {\sqrt {B_{{xy}}^2 + B_{{yy}}^2 + B_{{{\textit{z}}y}}^2} }\;,\\ {\sqrt {B_{{x{\textit{z}}}}^2 + B_{{y{\textit{z}}}}^2 + B_{{{\textit{z}}{\textit{z}}}}^2} }\;,\\ {\sqrt {B_{{xx}}^2 + B_{{yx}}^2 + B_{{{\textit{z}}x}}^2 + B_{{xy}}^2 + B_{{yy}}^2 + B_{{{\textit{z}}y}}^2} }\;,\\ {\sqrt {B_{{xx}}^2 + B_{{yx}}^2 + B_{{{\textit{z}}x}}^2 + B_{{x{\textit{z}}}}^2 + B_{{y{\textit{z}}}}^2 + B_{{{\textit{z}}{\textit{z}}}}^2} }\;,\\ {\sqrt {B_{{xy}}^2 + B_{{yy}}^2 + B_{{{\textit{z}}y}}^2 + B_{{x{\textit{z}}}}^2 + B_{{y{\textit{z}}}}^2 + B_{{{\textit{z}}{\textit{z}}}}^2} }\;. \end{array}} \right. (6) 通过上式计算磁场梯度张量的局部模量,即磁场梯度张量局部缩并,将磁场梯度张量G中的部分梯度参数缩并为标量{C_{\rm{n}}},即{C_{{x}}}、{C_{{y}}}、{C_{{{\textit{z}}}}}、{C_{{xy}}}、{C_{{x{\textit{z}}}}}和{C_{{y{\textit{z}}}}}. 局部模量仅使用部分梯度参量,当应用在锈蚀测试时,测量的参量更少、需要的磁传感器更少、使用更方便.
磁场梯度张量局部模量与铁磁构件的磁矩及测试距离的关系[14]为
{C_{\rm{n}}} = {k_{\rm{n}}}\frac{{{\mu _0}M}}{{4{\text{π}} {r^4}}}, (7) 式中:{C_{\rm{n}}}可选择6个局部模量中的任一个;{\mu _0}为介质磁导率;r为钢筋横截面的几何中心至磁场传感器几何中心的距离;M为铁磁构件(钢筋)的磁矩;{k_{\rm{n}}}为6个局部模量分别对应的6个参数[14].
钢筋的磁矩为
M = {M_0}V = {M_0}\frac{{{\text{π}} {D^2}}}{4}l = {M_0}\frac{m}{\rho }, (8) 式中:{M_0}、V、m、\rho 、D和 l 分别为单根钢筋的磁化强度、体积、质量、密度、直径及长度.
由式(7)、(8)可得钢筋的质量与磁场梯度局部模量之间的关系为
m = \frac{{4{\text{π}} {r^4}\rho {C_{\rm{n}}}}}{{{k_{\rm{n}}}{\mu _0}{M_0}}}. (9) 如在测量时保持r及传感器的朝向不变,则参数{k_{\rm{n}}}在锈蚀前后恒定;假定铁磁构件锈蚀后剩余部分的密度及磁化强度保持不变,则根据式(9)可认为{C_{\rm{n}}}与其质量成m正比.
根据钢筋锈蚀前、后的磁场梯度张量局部模量{C_{\rm{n0}}}和{C_{\rm{nc}}},由式(9)简化后用于钢筋的锈蚀率\eta (即失重率)评价,如式(10).
\eta = 1 - \xi \frac{{E\left( {{C_{\rm{nc}}}} \right)}}{{E\left( {{C_{\rm{n0}}}} \right)}}, (10) 式中:{C_{\rm{n0}}}和{C_{\rm{nc}}}可为6个局部模量中的任意一种局部模量;\xi 为测试时的距离修正系数,如式(11);E\left( {·} \right)为某变量在铁磁构件(钢筋)全长的平均值,后同.
\xi = {\left( {\frac{{{s_0}}}{{{s_{\rm{c}}}}}} \right)^4}, (11) 式中:s0和{s_{\rm{c}}}分别为锈蚀前、后测试时钢筋横截面中心至磁场传感器几何中心的距离.
本文中,锈蚀前、后测试时距离相等,\xi 取1.0.
2. 基于磁场梯度张量局部模量的钢筋锈蚀监测试验
2.1 试验材料及试件制作
采用全浸泡通电加速锈蚀试验模拟钢筋锈蚀,8根钢筋长度约为500 mm,钢筋规格为HPB300,配制浓度为8%的NaCl溶液. 本文主要研究钢筋锈蚀的监测方法,不专门设计锈蚀率,仅需得到不同程度的锈蚀率. 8根试件的具体参数见表1. 表1中:D0、l0、m0和t分别为初始直径、初始长度、初始质量和锈蚀时间.
表 1 试件设计Table 1. Specimen design编号 D0/mm l0/m m0/g t/d 1 9.54 503 278.74 4 2 9.43 481 261.81 4 3 9.43 484 265.83 4 4 9.39 485 266.93 4 5 9.48 504 275.56 4 6 9.44 495 272.38 4 7 9.72 500 277.48 5 8 9.60 496 274.91 5 2.2 通电加速锈蚀方法
采用通电加速锈蚀模拟钢筋的锈蚀程度,8根钢筋置于同一个水槽中. 待锈蚀的试件浸没在NaCl溶液之中,通过导线连接直流稳压电源的正极. 1根石墨碳棒浸泡在NaCl溶液且置于水槽边缘,与直流稳压电源的负极连接. 电流强度为1.0 A,电压为10 V,均在合理范围之内[18].
2.3 钢筋锈蚀的磁场测试
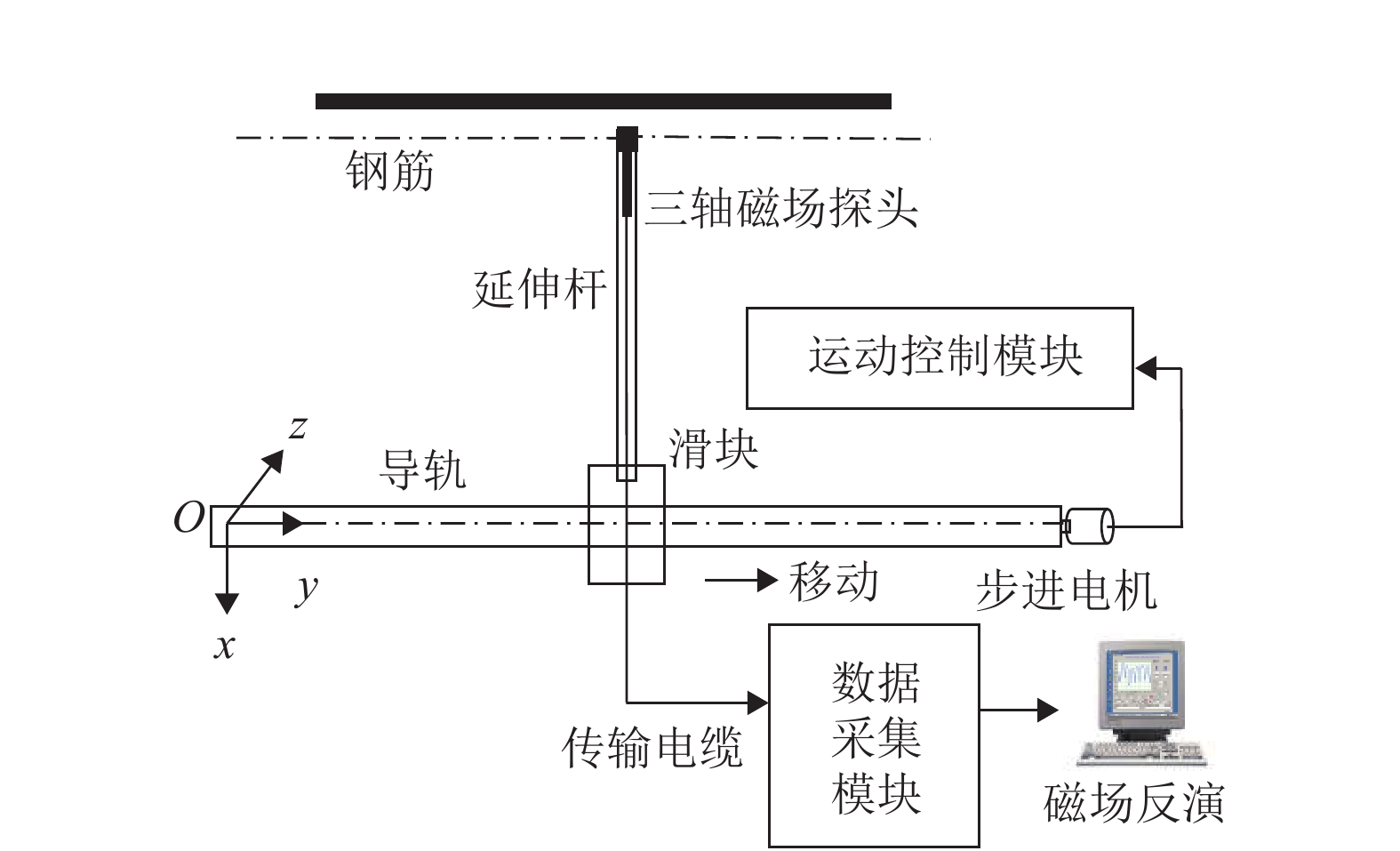
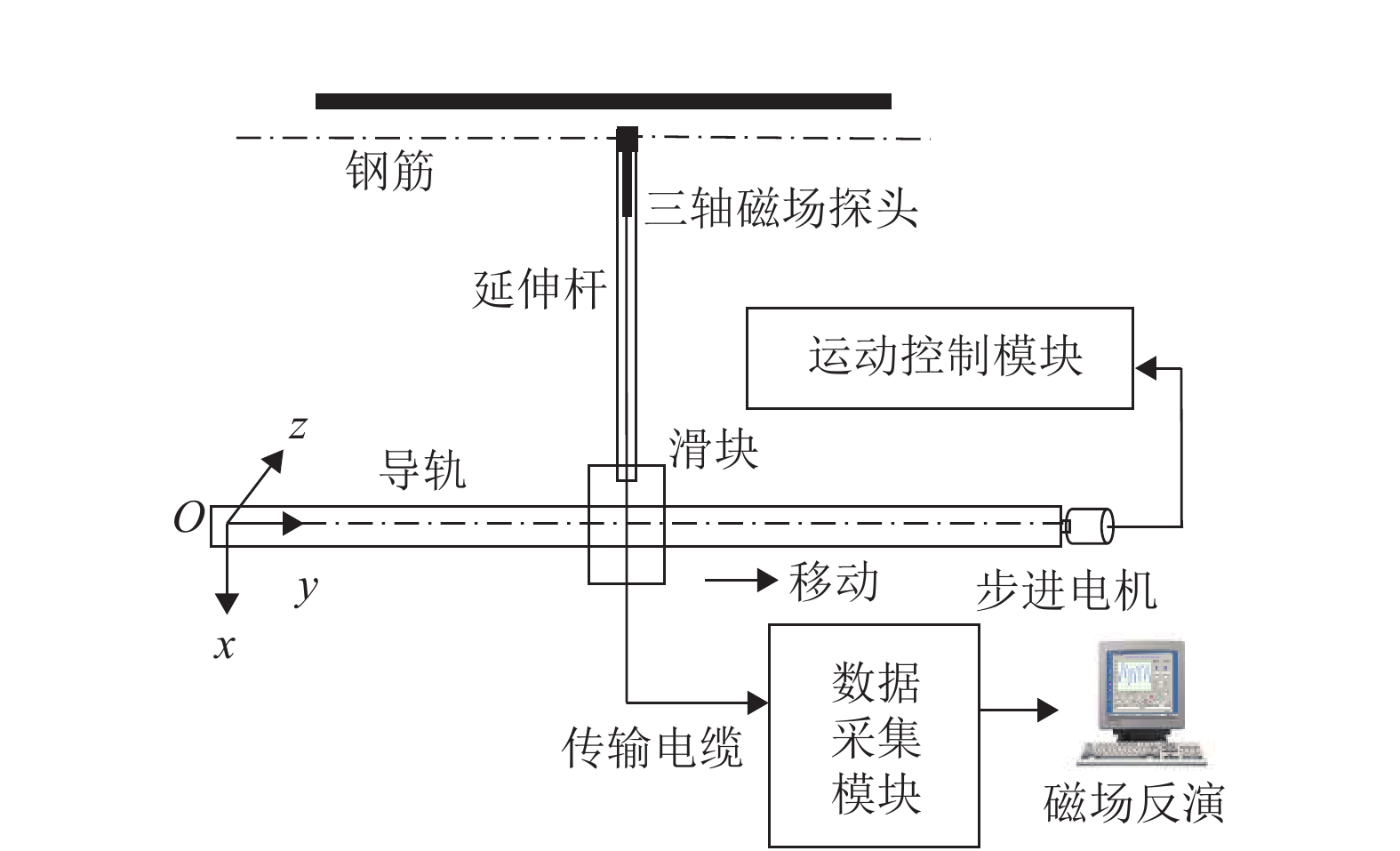
基于磁场梯度张量局部模量的钢筋锈蚀监测试验系统包括高精度运动控制平台和三轴磁通门磁力仪. 三轴磁通门磁力仪的探头沿着钢筋每隔1.8 mm测试一次磁感应强度. 锈蚀监测的试验系统见图1. 设置坐标系方向为:钢筋的长度方向为y方向,垂直于钢筋的长度且位于水平面内为x方向,垂直于钢筋的长度且位于铅垂面内为z方向.
从钢筋的端部开始在测点n处测量三轴磁感应强度{B_{{{x}},{{n}}}}、{B_{{{y}},{{n}}}}和{B_{{{{\textit{z}}}},{{n}}}},则磁场梯度为
{B_{{{xy}},{{n}}}} = \frac{{{B_{{{x}},{{n}}}} - {B_{{{x}},{{n}} + 1}}}}{d}, (12) {B_{{{yy}},{{n}}}} = \frac{{{B_{{{y}},{{n}}}} - {B_{{{y}},{{n}} + 1}}}}{d}, (13) {B_{{{{\textit{z}}y}},{{n}}}} = \frac{{{B_{{{{\textit{z}}}},{{n}}}} - {B_{{{{\textit{z}}}},{{n}} + 1}}}}{d}, (14) 式中:d为采样距离.
在测点n处,由式(6)计算磁场梯度张量的局部模量为
{C_{{{y}},{{n}}}} = \sqrt {B_{{{xy}},{{n}}}^2 + B_{{{yy}},{{n}}}^2 + B_{{{{\textit{z}}y}},{{n}}}^2} . (15) 当三轴磁场探头方向改变,或者设置多个三轴磁场探头时,同样可以通过式(6)计算得到磁场梯度局部模量.
测点n在钢筋上的位置为
L = dn = 1.8n. (16) 将{C_{{{y}},{{n}}}}代入式(10)、(11),计算钢筋锈蚀率,进行锈蚀损伤评价.
3. 通电锈蚀的试验结果分析
在通电锈蚀一定时间后,取出钢筋,然后用酸溶液清洗净,待干燥后称重,计算其失重率\zeta (\zeta = {{{{m_0} - {m_{\rm{c}}}} / {{m_0}}}},{m_{\rm{c}}}为锈蚀后的质量). 锈蚀前后各构件参数的对比见表2. 表2中:Dc、lc分别为锈蚀后的直径、长度.
表 2 钢筋锈蚀前后对比Table 2. Comparison before and after corrosion编号 D0/mm Dc/mm l0/mm lc/mm m0/g mc/g ζ/% 1 9.54 7.90 503 498 278.74 201.70 27.64 2 9.43 8.82 481 478 261.81 237.87 9.14 3 9.43 7.99 484 480 265.83 181.57 31.70 4 9.39 9.19 485 481 266.93 244.68 8.34 5 9.48 8.85 504 502 275.56 231.47 16.00 6 9.44 9.08 495 492 272.38 249.73 8.32 7 9.72 8.88 500 499 277.48 237.56 14.39 8 9.60 9.08 496 491 274.91 249.26 9.33 由表2可知:虽然部分试件在同样NaCl浓度的水槽中通电锈蚀同样的时间,但是失重率存在偏差,究其原因,在通电加速锈蚀过程中,钢筋表面积累铁锈,钢筋与电线的连接处及钢筋和电线与石墨碳棒连接处的接触电阻增大,离子迁移速度减缓,导致锈蚀速度降低,但不同试件锈蚀速度的降低程度不同,导致在同样的NaCl浓度和同样的锈蚀时间下,失重量存在偏差,且偏差较大,与相关文献[19]的现象一致.
4. 磁场测试的试验结果及分析
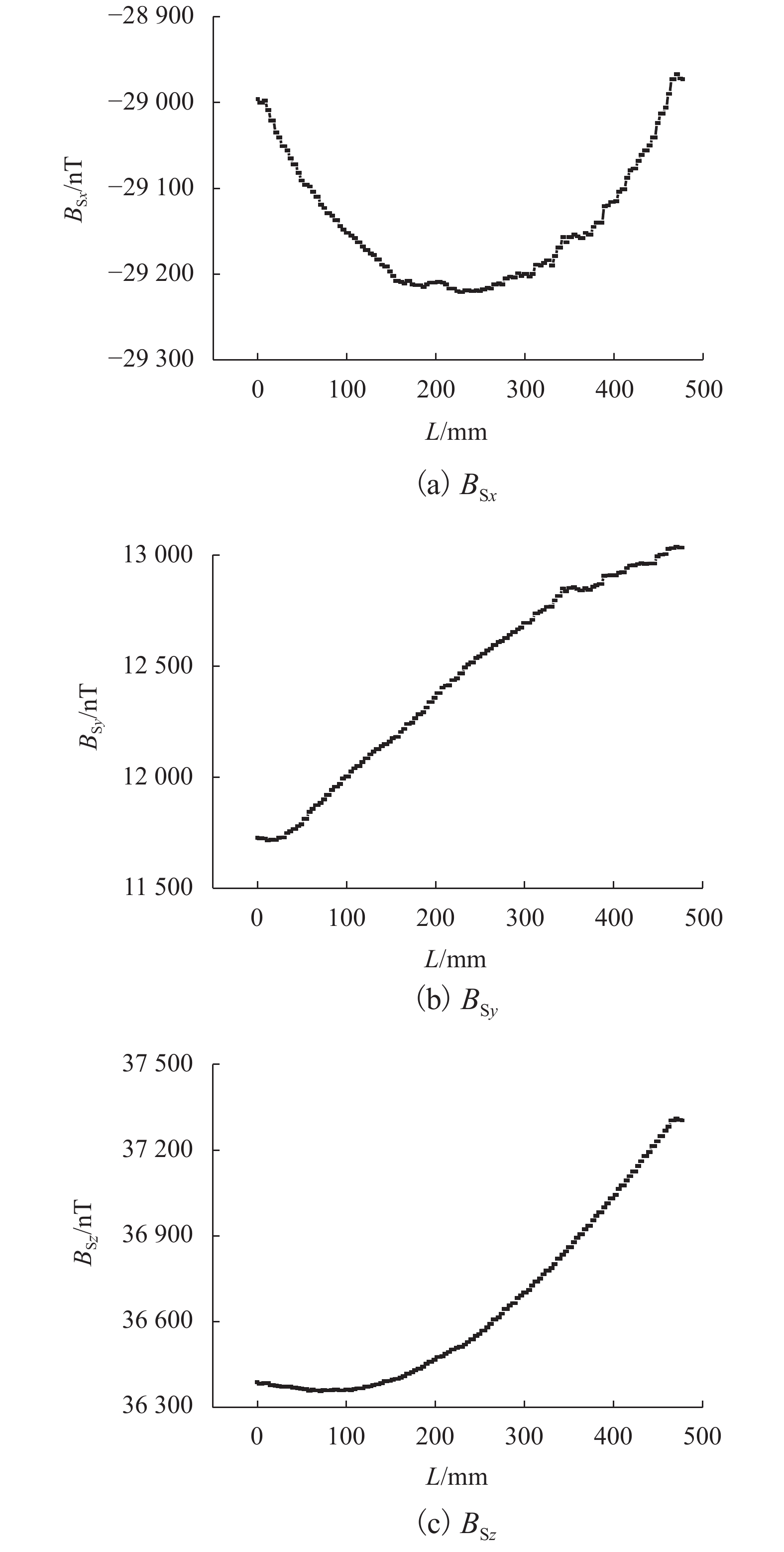
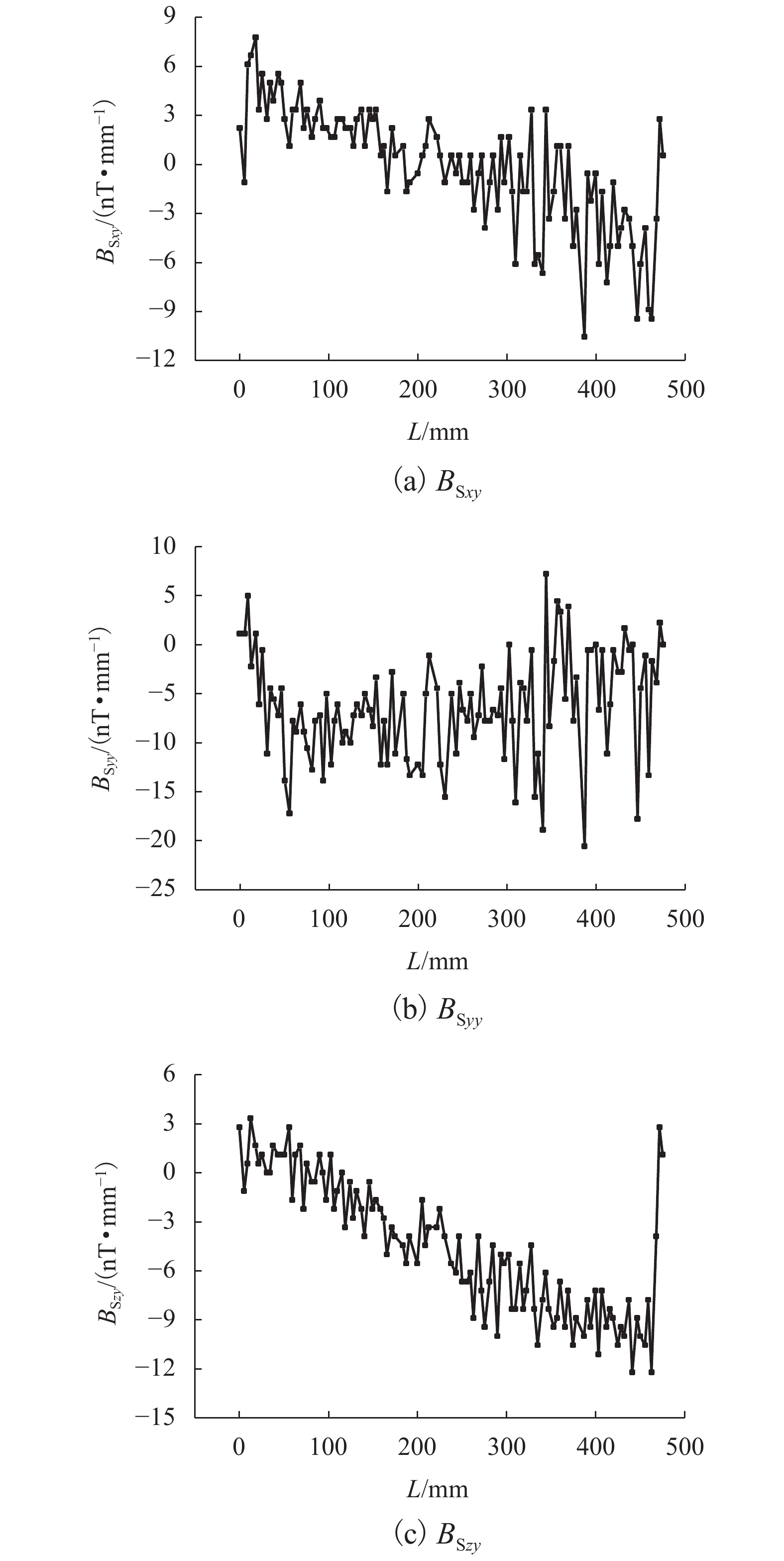
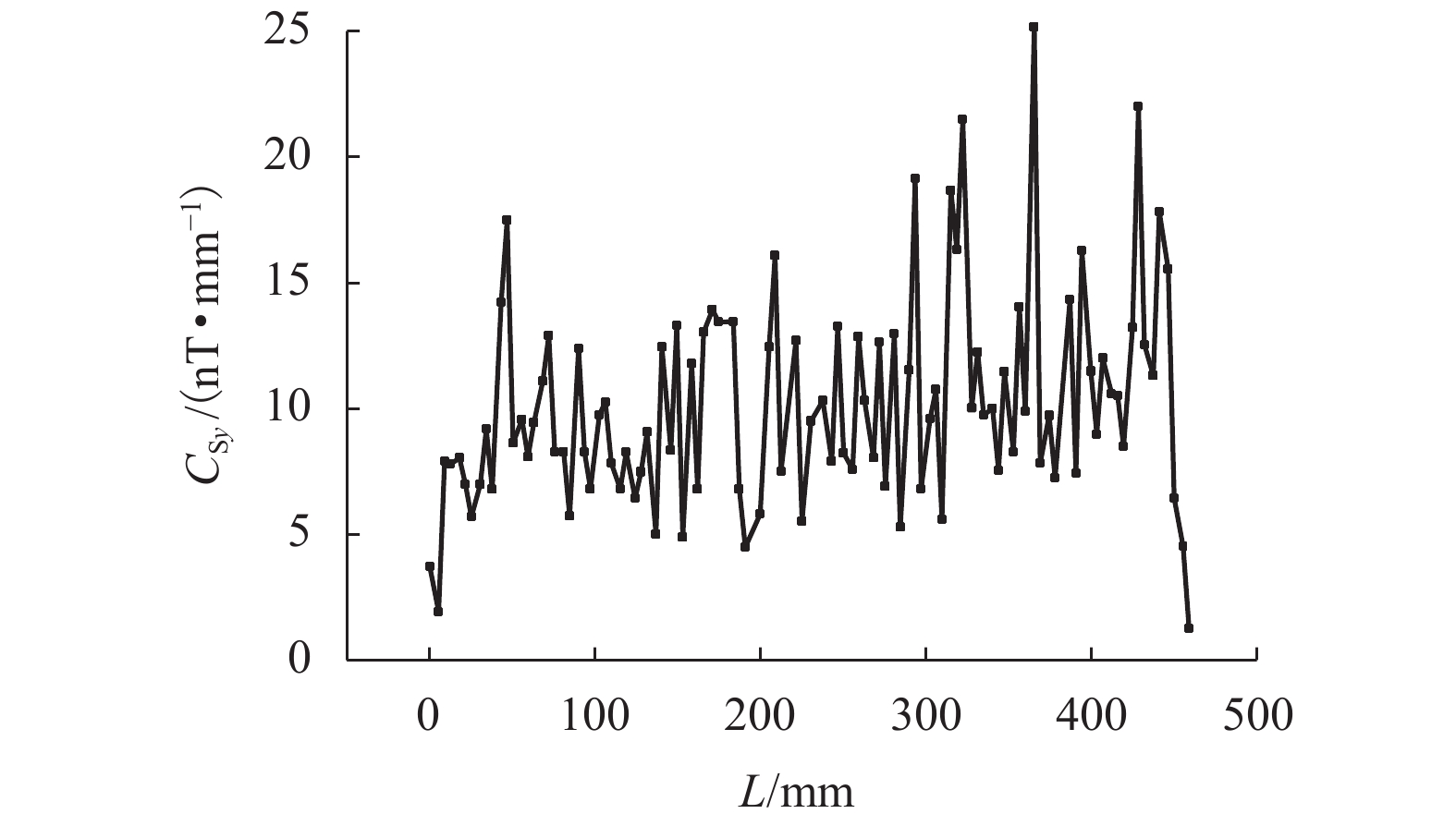
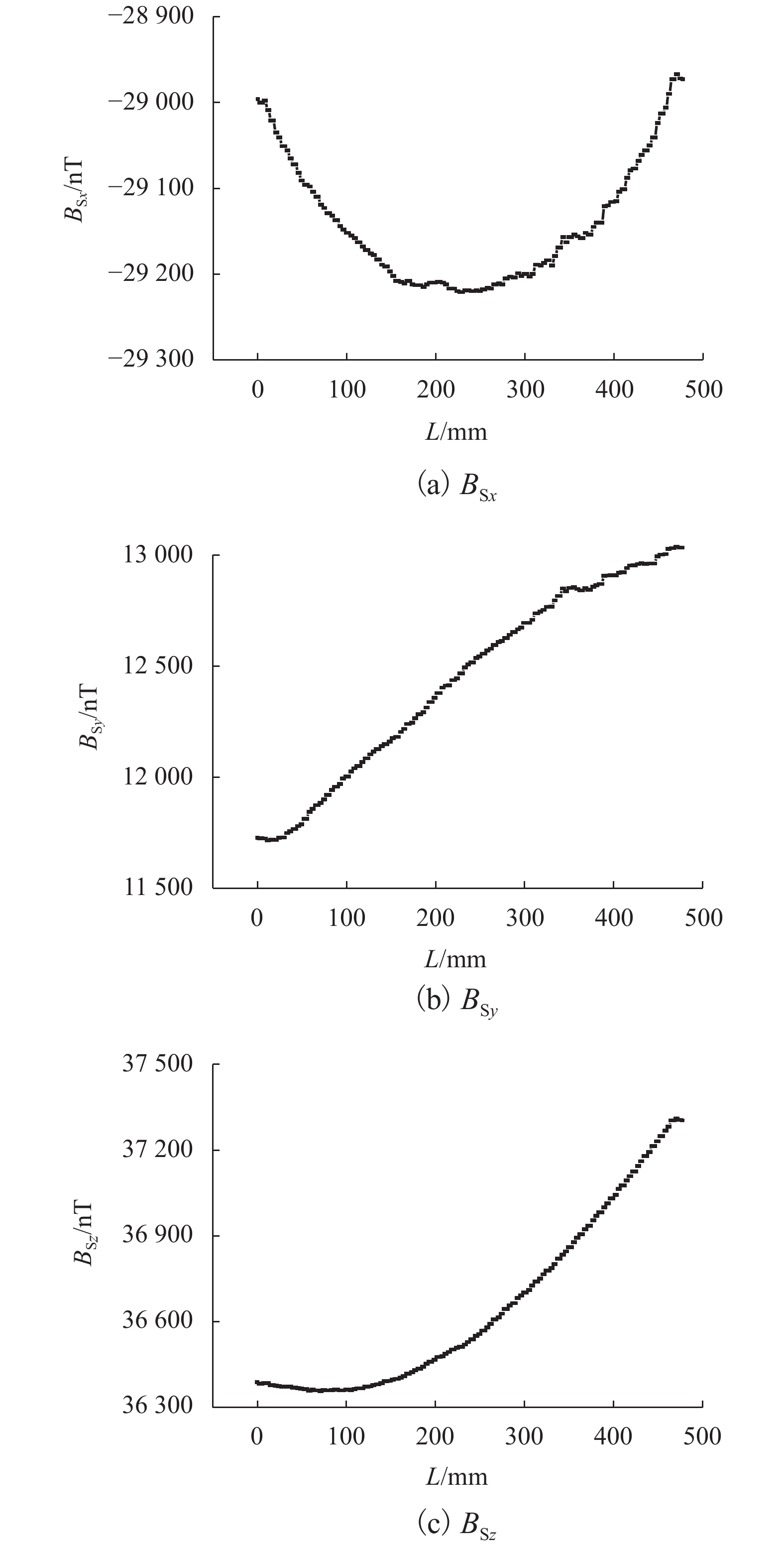
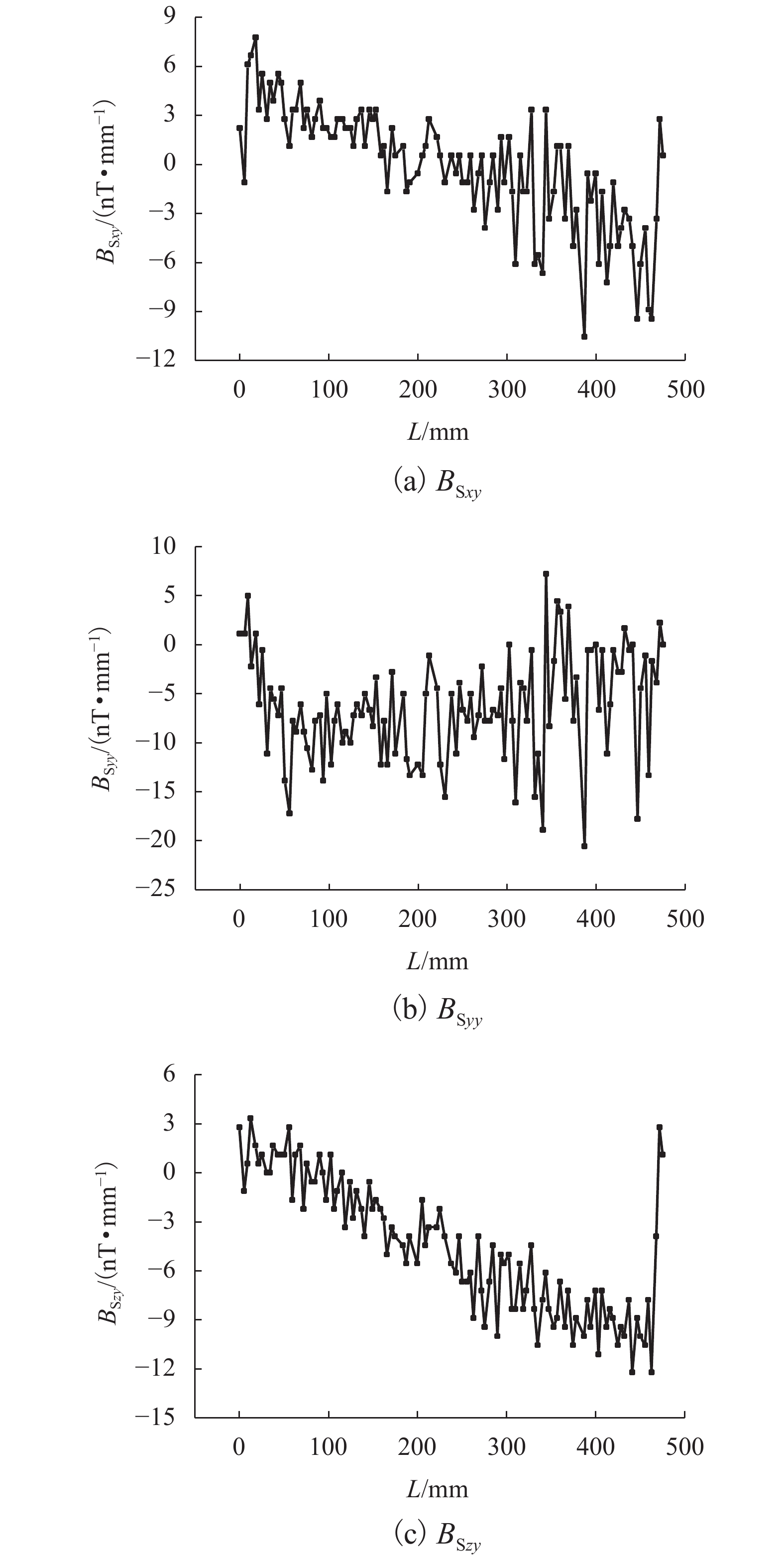
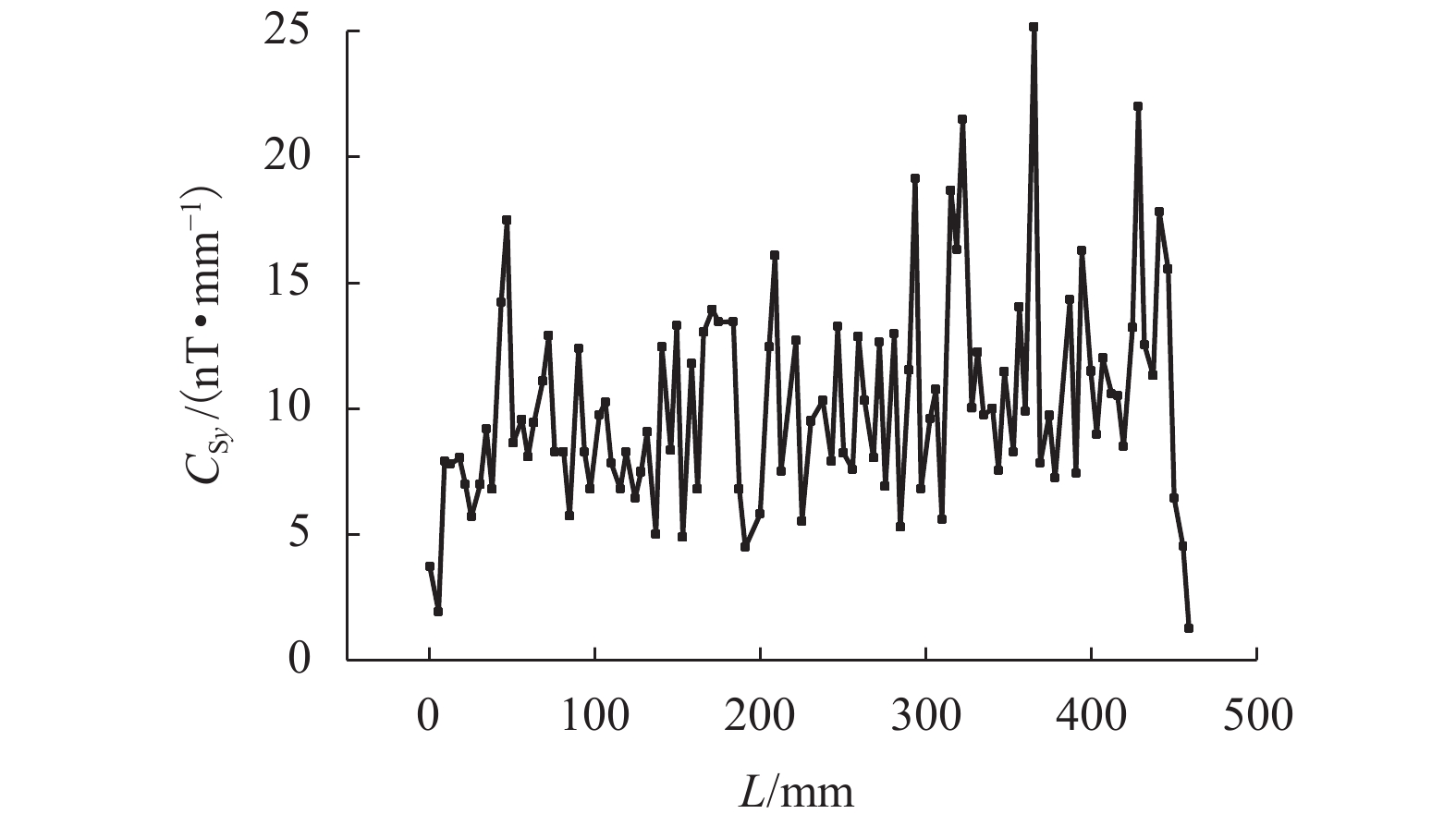
为分析环境磁场的影响,保持测试器件及测试地点不变的情况下,在三轴磁场探头处不放置钢筋,即处于空置状态,测试环境磁场的磁感强度为{B_{{\rm{S}}x}}、{B_{{\rm{S}}y}}和{B_{{\rm{S}}{\textit{z}}}},扫描长度大约为500 mm. 环境磁场的磁感应强度、梯度(BSxy、BSyy、BSzy)及局部模量(CSy)在长度范围内的曲线关系见图2~4. 环境磁场参数的绝对值在扫描长度内的平均值见表3.
表 3 环境磁场参数绝对值的平均值Table 3. Average absolute values of environmental magneticE\left( {\left| { {B_{{\rm{S} }x} } } \right|} \right)/nT E\left( {| { {B_{{\rm{S} }y} } } |} \right)/nT E\left( {\left| { {B_{{\rm{S} }{\textit{z}}} } } \right|} \right)/nT E\left( {| { {B_{{\rm{S} }xy} } } |} \right)/(nT•mm−1) E\left( {| { {B_{{\rm{S}}yy} } }|} \right)/(nT•mm−1) E\left( {| { {B_{{\rm{S}}{\textit{z}}y} } } |} \right)/(nT•mm−1) E\left( { { {C_{{\rm{S} }y}} } } \right)/(nT•mm−1) 29142 12439 36654 2.92 6.88 5.01 10.14 由图2和表3可得:在本试验中,{B_{{\rm{S}}x}}、{B_{{\rm{S}}y}}及{B_{{\rm{S}}{\textit{z}}}}的绝对值的平均值,变化幅度大约分别在400、150 nT和1 200 nT的范围之内. 环境磁场由地球背景磁场及环境干扰磁场组成,其中,地球背景磁场的磁感应强度在数值上较大,但在短距离内(本文中L = 500 mm)变化极小;环境干扰磁场主要为高精度运动控制平台中的导轨、步进电机等部件,环境干扰磁场的磁感应强度在数值上较小,但在短距离内(本文中L = 500 mm)存在一定的变化;地球背景磁场及环境干扰磁场这两种磁场矢量叠加后,总的环境磁场的磁感应强度在扫描测试长度范围之内存在较大幅度的变化. 可见,如采用磁感应强度进行钢筋锈蚀监测,环境磁场不可忽略,需要分离环境磁场得到钢筋自身的磁场.
由图3和表3可得:在本试验中,环境磁场的梯度{B_{{{\rm{S}}xy}}}、{B_{{{\rm{S}}yy}}}及{B_{{{\rm{S}}{\textit{z}}y}}}分别在−12~9 nT/mm,−21~10 nT/mm和−15~6 nT/mm的范围之内,绝对值的平均值分别为2.92、6.88 nT/mm和5.01 nT/mm. 地球磁场梯度的垂向约20 × 10−6 nT/mm,水平约5 × 10−6 nT/mm,因此,对于环境磁场的梯度值,地球背景磁场的梯度可忽略不计,环境磁场的梯度值主要为环境干扰磁场的梯度. 本文中,环境干扰磁场为高精度运动控制平台中步进电机等部件激发的磁场.
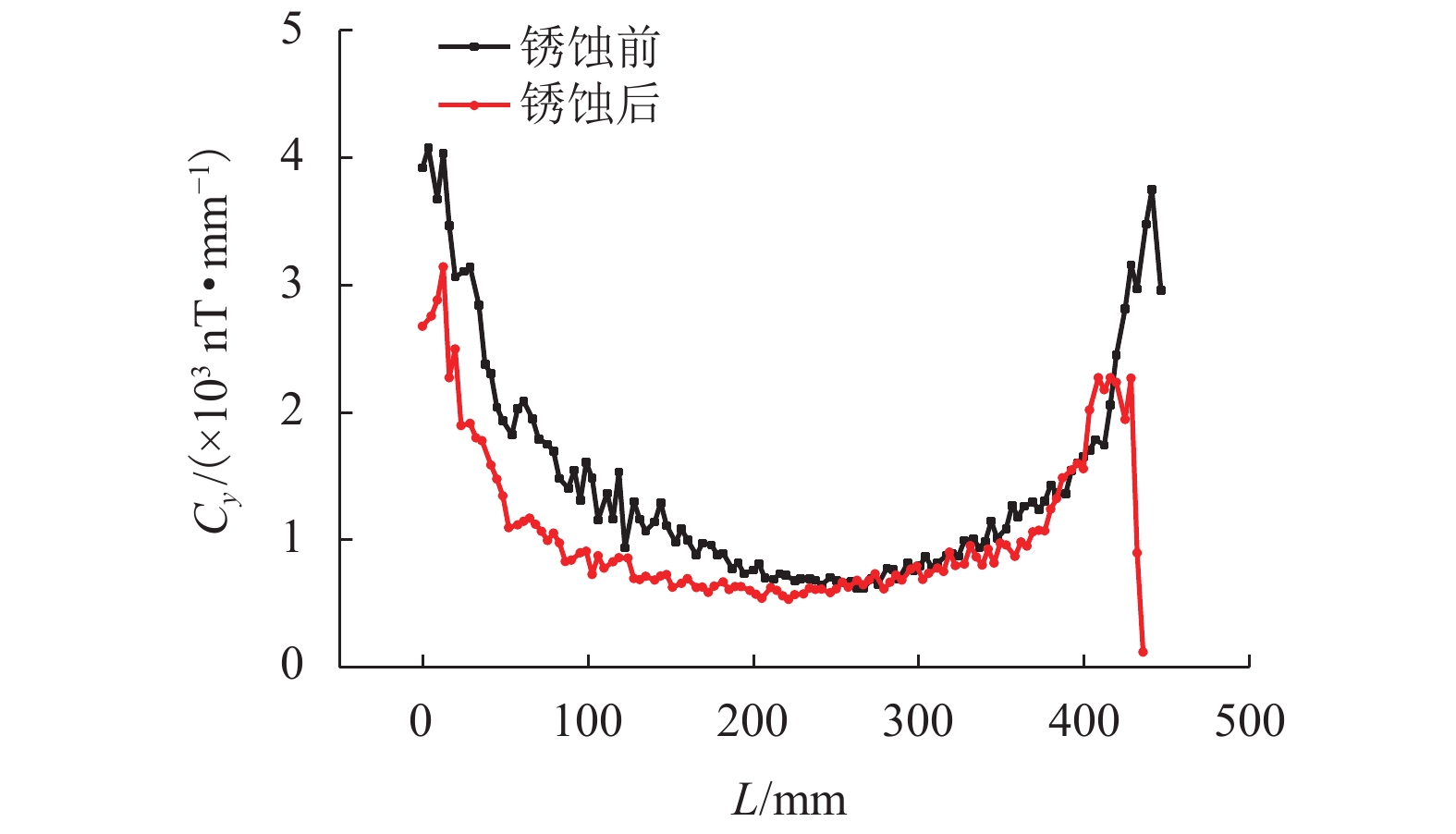
由图4和表3可得:在本试验中,{C_{{\rm{S}}y}}在0~25 nT•mm−1的范围之内,平均值为10.14 nT•mm−1. 由于地球背景磁场的梯度极小,相应的磁场梯度局部模量忽略不计,显而易见,上述测得的环境磁场的磁场梯度局部模量主要为环境干扰磁场激发.
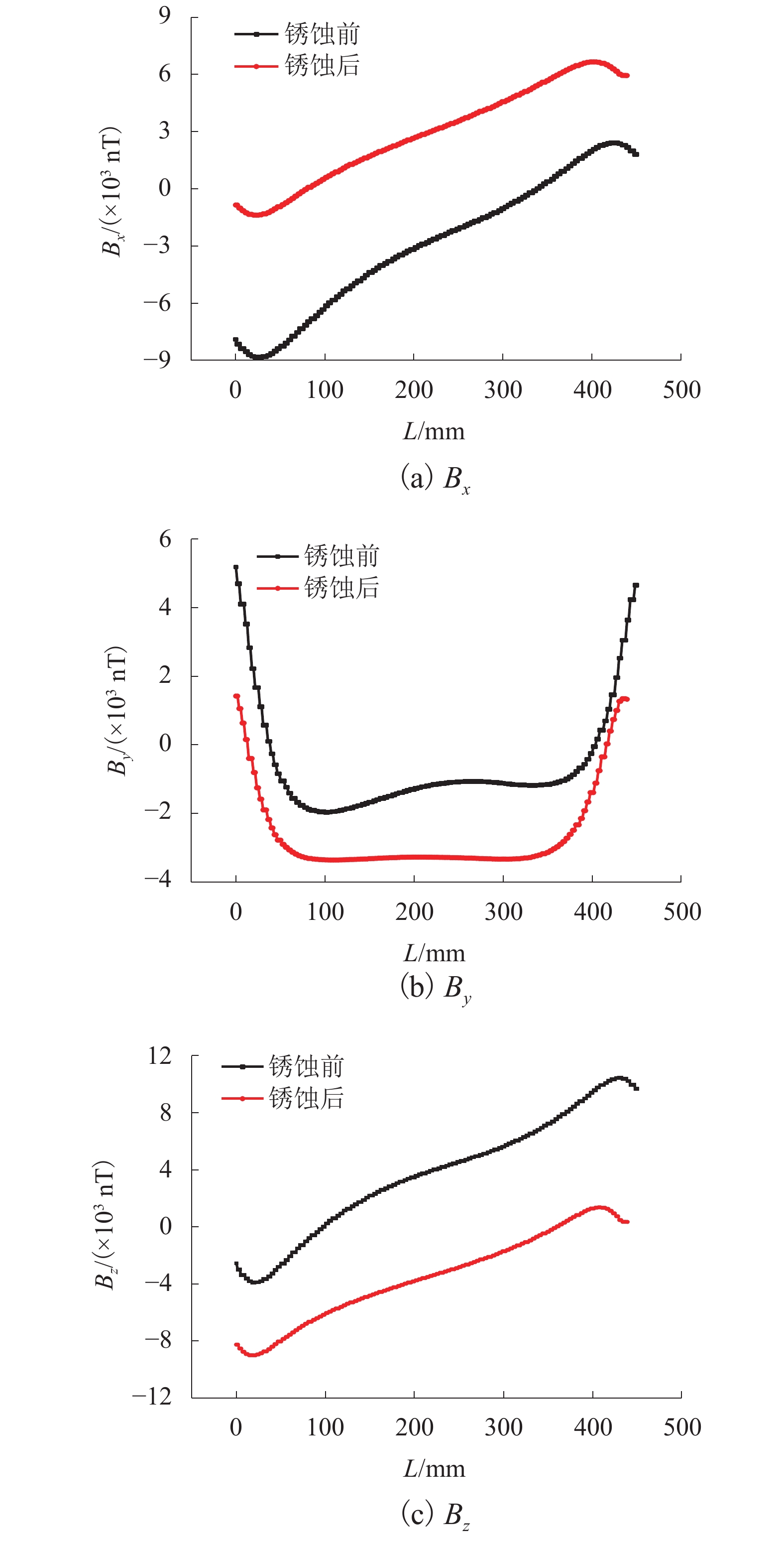
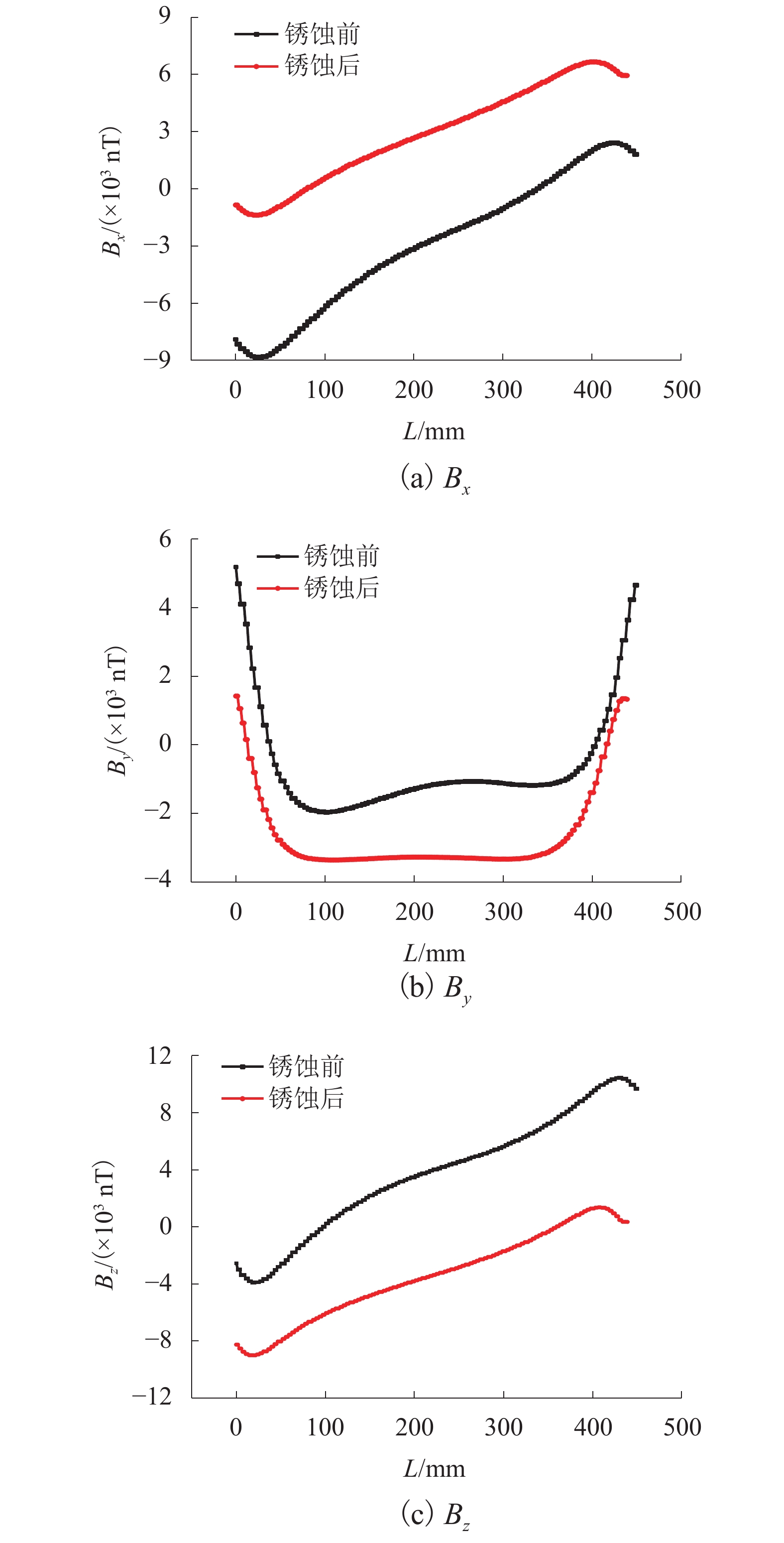
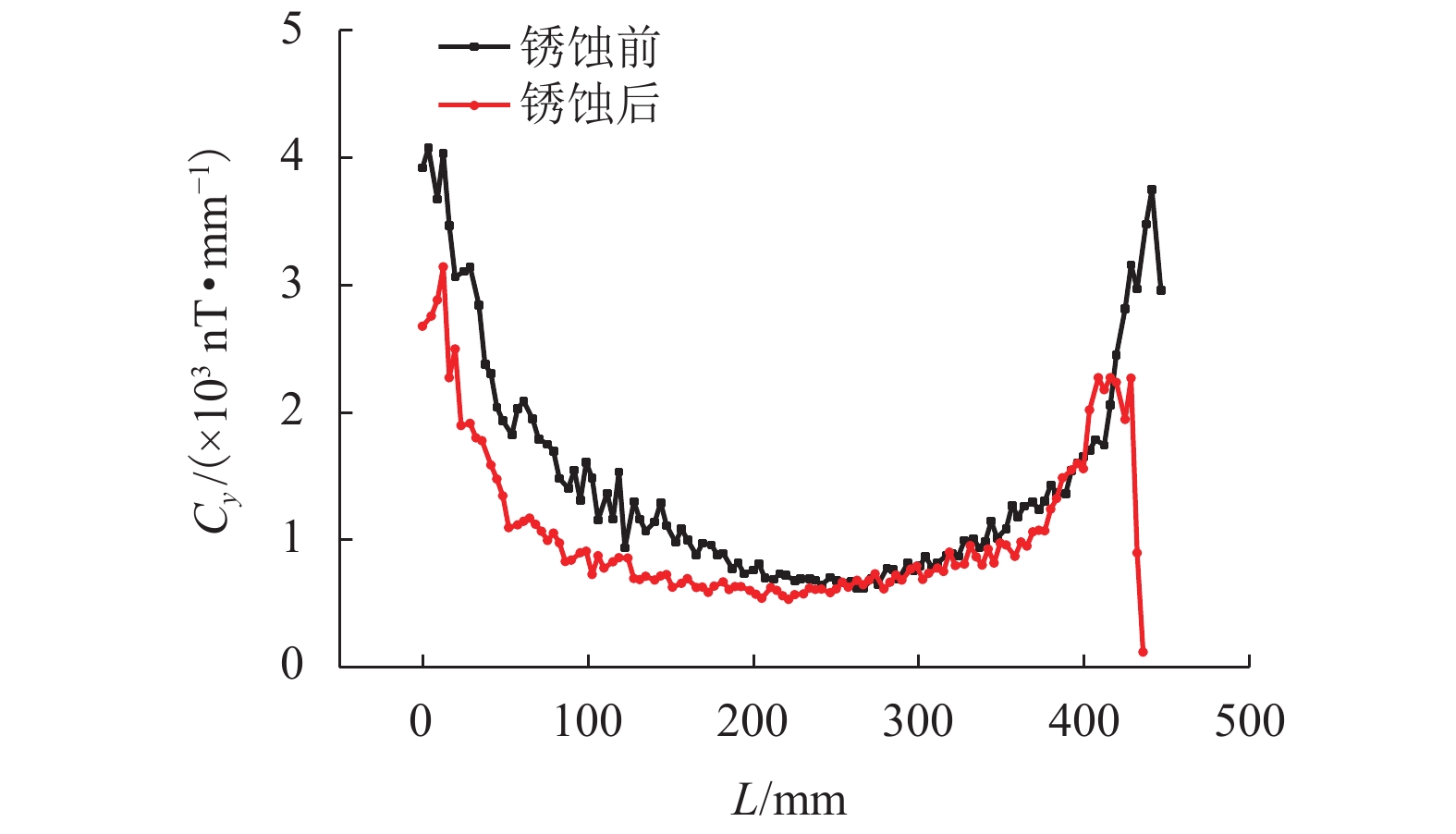
测试得到钢筋各测点处的磁感应强度,计算各测点处的磁场梯度,得到锈蚀前后钢筋全长的磁感应强度、磁场梯度和局部模量随钢筋位置的曲线关系,鉴于8根试件的曲线规律基本相同,仅给出1号钢筋的曲线图,见图5~7.
由图5可知:1){B_{{x}}}和{B_{\textit{z}}}的分布规律相同,均为拉长的S形,{B_{{y}}}分布规律为扁平的W形(或M形);2) 锈蚀后钢筋的磁感应强度随长度方向变化的曲线更光滑,斜率降低,即磁场梯度的绝对值减小;3) 锈蚀后钢筋的磁感应强度({B_{{x}}}、{B_{{y}}}和{B_{\textit{z}}})曲线,发生非等距离的偏移,究其原因,测试得到的磁感应强度由环境磁场和钢筋自身磁场叠加而成,锈蚀后钢筋自身磁感应强度的绝对值减小;且钢筋锈蚀程度并非完全的均匀;4) 钢筋部分测点位置,锈蚀后的磁感应强度的绝对值,小于锈蚀前的磁感应强度,但也有很大一部分测点锈蚀后的磁感应强度绝对值大于锈蚀前,没有一致性的规律,究其原因,钢筋锈蚀后,钢筋自身的磁感应强度的绝对值均减小. 由于钢筋自身的磁感应强度{\boldsymbol{B}}在长度范围内方向发生改变,且钢筋有些测点的磁感应强度绝对值会大于环境磁场的磁感应强度{{\boldsymbol{B}}_{\rm{S}}}的绝对值,而有些测点的磁感应强度绝对值会小于环境磁场的磁感应强度{{\boldsymbol{B}}_{\rm{S}}}的绝对值. 以x方向为例,扫描测试的总磁感应强度{{\boldsymbol{B}}_{\rm{T}}} = {\boldsymbol{B}} + {{\boldsymbol{B}}_{\rm{S}}}分以下3种情况讨论:① 如果钢筋自身的磁感应强度{B_{{x}}}和环境磁场的磁感应强度{B_{{\rm{S}}x}}方向相同(均为正或负),则锈蚀后,测试的总磁感应强度的绝对值为\left| {{B_{{\rm{T}}x}}} \right| = \left| {{B_{{x}}}} \right| + \left| {{B_{{\rm{S}}x}}} \right|,由于钢筋自身的磁感应强度绝对值\left| {{B_{{x}}}} \right|减小,所以锈蚀后,测试的总磁感应强度的绝对值\left| {{B_{{\rm{T}}x}}} \right|减小. ② 如果钢筋自身的磁感应强度{B_{{x}}}和环境磁场的磁感应强度{B_{{\rm{S}}x}}方向相反(一正一负),但钢筋自身的磁感应强度绝对值\left| {{B_{{x}}}} \right|大于环境的磁感应强度绝对值\left| {{B_{{\rm{S}}x}}} \right|,则锈蚀后,测试的总磁感应强度的绝对值为\left| {{B_{{\rm{T}}x}}} \right| = \left| {{B_{{x}}}} \right| - \left| {{B_{{\rm{S}}x}}} \right|,由于钢筋自身的磁感应强度绝对值\left| {{B_{{x}}}} \right|减小,所以锈蚀后,测试的总磁感应强度的绝对值\left| {{B_{{\rm{T}}x}}} \right|减小. ③ 如果钢筋自身的磁感应强度{B_{{x}}}和环境磁场的磁感应强度{B_{{\rm{S}}x}}方向相反(一正一负),但钢筋自身的磁感应强度绝对值\left| {{B_{{x}}}} \right|小于环境的磁感应强度绝对值\left| {{B_{{\rm{S}}x}}} \right|,则锈蚀后,测试的总磁感应强度的绝对值为\left| {{B_{{\rm{T}}x}}} \right| = \left| {{B_{{\rm{S}}x}}} \right| - \left| {{B_{{x}}}} \right|,由于钢筋自身的磁感应强度绝对值\left| {{B_{{x}}}} \right|减小,所以锈蚀后,测试的总磁感应强度的绝对值\left| {{B_{{\rm{T}}x}}} \right|增大.
因此,钢筋锈蚀后,直接通过磁场传感器测试的磁感应强度绝对值可能会增大,也可能会减小,没有一致性的规律. 如采用磁感应强度进行钢筋锈蚀监测,需要解决从测试的总磁感应强度中分离环境磁场的难题. 但地球背景磁场和环境干扰磁场等环境磁场随时间发生变化,实际中很难测量得到钢筋自身的磁感应强度.
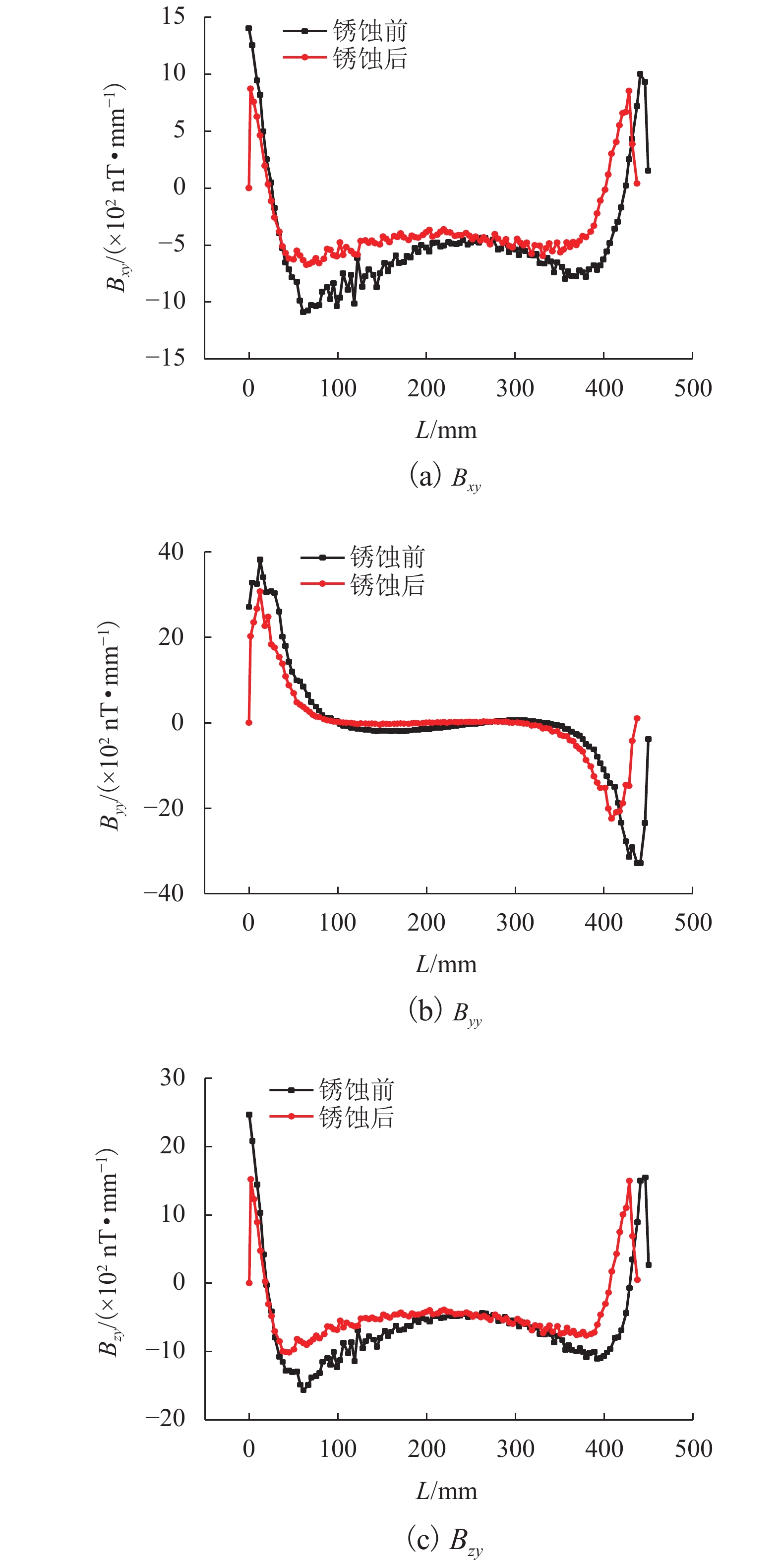
由图6可知:1) 钢筋的磁场梯度{B_{{xy}}}和{B_{{{\textit{z}}y}}}的分布规律一致,即均为W形,中间平缓而两端突变,不同于{B_{{yy}}}的分布规律;2) 锈蚀后钢筋的大部分测点处磁场梯度的绝对值减少,且减少的幅度较明显.
由图7可知:锈蚀后钢筋几乎所有测点位置的磁场梯度局部模量减小,仅有极个别测点处的磁场梯度局部模量增大.
1号钢筋锈蚀前后的磁感应强度、磁场梯度及局部模量在全长度上平均值的对比见表4.
表 4 1号钢筋锈蚀前后磁场参数的平均值对比Table 4. Comparison of average values of magnetic parameters before and after corrosion of specimen No. 1项目 E(|Bx|)/nT E(|By|)/nT E(|Bz|)/nT E(|Bxy|)/(nT•mm−1) E(|Byy|)/(nT•mm−1) E(|Bzy|)/(nT•mm−1) E(Cy)/(nT•mm−1) 锈蚀前 36684.76 14767.02 47463.04 647.70 709.75 832.91 1464.17 锈蚀后 32380.07 27619.37 38090.48 468.86 489.32 615.00 1062.76 锈蚀后/
锈蚀前0.882 7 1.870 3 0.822 5 0.723 9 0.689 4 0.738 4 0.725 8 由表4结合表3可知:1) 在锈蚀后1号钢筋的磁感应强度绝对值有增大也有降低,没有一致性的规律,前文已阐述理由;2) 在锈蚀后1号钢筋磁场梯度绝对值及局部模量的平均值均小于锈蚀前;3) 测量的磁感应强度实际上为钢筋和环境磁场两者的矢量叠加,平均值约15 000 ~ 47 000 nT,而前述测得的环境磁场(包括地球背景磁场和环境干扰磁场)的磁感应强度绝对值的平均值为12 439~336654 nT,如采用磁感应强度评价钢筋的锈蚀程度,环境磁场的分离及瞬态效应是一个无法避免且异常困难的问题;4) 钢筋磁场梯度绝对值的平均值(约为300~800 nT/mm),数百倍于环境磁场的磁场梯度(绝对值平均值约为2.92~6.88 nT/mm),所以,测试钢筋锈蚀时,可忽略环境磁场的梯度;5) 钢筋锈蚀测试的磁场梯度局部模量(1000~1500 nT/mm),数百倍于环境磁场的磁场梯度局部模量(10.14 nT/mm),可忽略环境磁场的磁场梯度局部模量.
地球磁场和环境干扰磁场的分离非常困难,且地球背景磁场和环境干扰磁场等环境磁场随时间发生变化,很难得到钢筋自身的磁感应强度,所以本文采用磁场梯度局部模量进行钢筋的锈蚀监测.
对于8根钢筋,采用磁场梯度局部模量{C_{{y}}}计算得到理论锈蚀率,则8根试件的理论锈蚀率\eta 与实测失重率(ζ)的对比见表5.
Table 5. Comparison of calculated and measured corrosion rates试件编号 η/% ζ/% 误差/% 1 27.42 27.64 0.22 2 12.46 9.14 3.32 3 41.10 31.70 9.40 4 16.00 8.34 7.66 5 18.75 16.00 2.75 6 9.02 8.32 0.70 7 8.83 14.39 5.56 8 11.11 9.33 1.78 由表5可知:8根钢筋的计算锈蚀率与实测失重率的最小误差为0.22%,最大误差为9.40%. 8根钢筋的误差平均值为3.92%,小于5%;误差的标准差为3.32%. 总体上计算锈蚀率与实测失重率基本一致,且误差的浮动和离散度较小. 在磁场梯度计算时截取钢筋的起止位置存在一定的人为主观经验,高精度运动控制平台和三轴磁通门磁力仪的同步控制需要进一步研究.
5. 结 论
1) 为了研究混凝土结构中钢筋锈蚀的无损及定量锈蚀监测方法,结合地球背景磁场和环境干扰磁场的影响,发展了钢筋的磁场梯度张量局部模量与锈蚀率之间的计算公式.
2) 通过8根钢筋进行加速锈蚀试验模拟钢筋的锈蚀,研制了磁场监测试验系统,测量锈蚀前后钢筋的磁感应强度,采用磁场梯度张量局部模量反演钢筋的锈蚀率.
3) 相比锈蚀前,钢筋锈蚀后测试的磁感应强度曲线发生非等距离的偏移,但绝对值有增大也有降低,没有一致性的规律;在钢筋锈蚀后磁场梯度绝对值和局部模量的平均值减小. 在钢筋锈蚀监测时,钢筋自身的磁场梯度及局部模量数百倍于环境磁场,环境磁场的梯度及其局部模量可忽略不计.
4) 磁场梯度局部模量计算得到的锈蚀率更加稳定可靠. 磁场梯度的局部模量包含了磁性体更多的信息,环境磁场的影响小,在进行锈蚀监测时更准确.
5) 8根钢筋的计算锈蚀率与实测失重率的最小误差为0.22%,最大误差为9.40%. 误差的平均值为3.92%,小于5.00%;误差的标准差为3.32%,总体上计算锈蚀率与实测失重率基本一致,且误差浮动较小.
6) 磁场梯度计算时截取构件的起止位置存在一定的人为主观经验,钢筋锈蚀监测的试验系统中高精度运动控制平台和三轴磁通门磁力仪的同步控制需要进一步研究.
-
表 1 试件设计
Table 1. Specimen design
编号 D0/mm l0/m m0/g t/d 1 9.54 503 278.74 4 2 9.43 481 261.81 4 3 9.43 484 265.83 4 4 9.39 485 266.93 4 5 9.48 504 275.56 4 6 9.44 495 272.38 4 7 9.72 500 277.48 5 8 9.60 496 274.91 5 表 2 钢筋锈蚀前后对比
Table 2. Comparison before and after corrosion
编号 D0/mm Dc/mm l0/mm lc/mm m0/g mc/g ζ/% 1 9.54 7.90 503 498 278.74 201.70 27.64 2 9.43 8.82 481 478 261.81 237.87 9.14 3 9.43 7.99 484 480 265.83 181.57 31.70 4 9.39 9.19 485 481 266.93 244.68 8.34 5 9.48 8.85 504 502 275.56 231.47 16.00 6 9.44 9.08 495 492 272.38 249.73 8.32 7 9.72 8.88 500 499 277.48 237.56 14.39 8 9.60 9.08 496 491 274.91 249.26 9.33 表 3 环境磁场参数绝对值的平均值
Table 3. Average absolute values of environmental magnetic
E\left( {\left| { {B_{{\rm{S} }x} } } \right|} \right)/nT E\left( {| { {B_{{\rm{S} }y} } } |} \right)/nT E\left( {\left| { {B_{{\rm{S} }{\textit{z}}} } } \right|} \right)/nT E\left( {| { {B_{{\rm{S} }xy} } } |} \right)/(nT•mm−1) E\left( {| { {B_{{\rm{S}}yy} } }|} \right)/(nT•mm−1) E\left( {| { {B_{{\rm{S}}{\textit{z}}y} } } |} \right)/(nT•mm−1) E\left( { { {C_{{\rm{S} }y}} } } \right)/(nT•mm−1) 29142 12439 36654 2.92 6.88 5.01 10.14 表 4 1号钢筋锈蚀前后磁场参数的平均值对比
Table 4. Comparison of average values of magnetic parameters before and after corrosion of specimen No. 1
项目 E(|Bx|)/nT E(|By|)/nT E(|Bz|)/nT E(|Bxy|)/(nT•mm−1) E(|Byy|)/(nT•mm−1) E(|Bzy|)/(nT•mm−1) E(Cy)/(nT•mm−1) 锈蚀前 36684.76 14767.02 47463.04 647.70 709.75 832.91 1464.17 锈蚀后 32380.07 27619.37 38090.48 468.86 489.32 615.00 1062.76 锈蚀后/
锈蚀前0.882 7 1.870 3 0.822 5 0.723 9 0.689 4 0.738 4 0.725 8 Table 5. Comparison of calculated and measured corrosion rates
试件编号 η/% ζ/% 误差/% 1 27.42 27.64 0.22 2 12.46 9.14 3.32 3 41.10 31.70 9.40 4 16.00 8.34 7.66 5 18.75 16.00 2.75 6 9.02 8.32 0.70 7 8.83 14.39 5.56 8 11.11 9.33 1.78 -
[1] 苏成光,刘丹,赵坪锐,等. 道床板钢筋锈蚀的细观力学影响[J]. 西南交通大学学报,2020,55(2): 273-281, 289.SU Chengguang, LIU Dan, ZHAO Pingrui, et al. Meso-mechanical effect of track slab rebar corrosion[J]. Journal of Southwest Jiaotong University, 2020, 55(2): 273-281, 289. [2] DOUBOV A A. Screening of weld quality using the magnetic metal memory effect[J]. Weld World, 1998, 41(3): 196-199. [3] DOUBOV A A. The express technique of welded joints examination with use of metal magnetic memory[J]. NDT & E International, 2000, 33(6): 351-362. [4] FERNANDES B, TITUS M, NIMS D K, et al. Field test of magnetic methods for corrosion detection in prestressing strands in adjacent box-beam bridges[J]. Journal of Bridge Engineering, 2012, 17(6): 984-988. doi: 10.1061/(ASCE)BE.1943-5592.0000379 [5] 陈海龙,王长龙,朱红运. 基于磁梯度张量的金属磁记忆检测方法[J]. 仪器仪表学报,2016,37(3): 602-609. doi: 10.3969/j.issn.0254-3087.2016.03.017CHEN Hailong, WANG Changlong, ZHU Hongyun. Metal magnetic memory test method based on magnetic gradient tensor[J]. Chinese Journal of Scientific Instrument, 2016, 37(3): 602-609. doi: 10.3969/j.issn.0254-3087.2016.03.017 [6] 马惠香,周建庭,赵瑞强,等. 基于金属磁记忆技术的钢筋应力无损检测试验[J]. 江苏大学学报(自然科学版),2018,39(3): 106-111.MA Huixiang, ZHOU Jianting, ZHAO Ruiqiang, et al. Non-destructive testing of steel bar stress based on metal magnetic memory technology[J]. Journal of Jiangsu University (Natural Science Edition), 2018, 39(3): 106-111. [7] WIEGERT R, OESCHGER J. Generalized magnetic gradient contraction based method for detection, localization and discrimination of underwater mines and unexploded ordnance[C]//Proceedings of Oceans 2005 MTS/IEEE. Washington D. C.: IEEE, 2005: 1-8 [8] WIEGERT R F, PURPURA J W. Magnetic scalar triangulation and ranging system for autonomous underwater vehicle based detection, localization and classification of magnetic mines[C]//Oceans. Kobe: IEEE, 2005: 890-896. [9] LIU R, WANG H. Detection and localization of improvised explosive devices based on 3-axis magnetic sensor array system[J]. Procedia Engineering, 2010, 7: 1-9. doi: 10.1016/j.proeng.2010.11.001 [10] SCHMIDT P W, CLARK D A. The magnetic gradient tensor:its properties and uses in source characterization[J]. Leading Edge, 2006, 25(1): 75-78. doi: 10.1190/1.2164759 [11] WIEGERT R, LEE K, OESCHGER J. Improved magnetic STAR methods for real-time, point-by-point localization of unexploded ordnance and buried mines[C]//Oceans. Quebec City: IEEE, 2008: 1-7. [12] WIEGERT R F. Magnetic STAR technology for real-time localization and classification of unexploded ordnance and buried mines[C]//Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XIV. Orlando: [s.n.], 2009: 73031U.1-73031U.19. [13] 江胜华,申宇,褚玉程. 基于磁偶极子的磁场梯度张量缩并的试验验证及相关参数确定[J]. 中国惯性技术学报,2015,23(1): 103-106,114.JIANG Shenghua, SHEN Yu, CHU Yucheng. Experimental verification and related parameter’s determination for magnetic gradient tensor contraction using magnetic dipole[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 103-106,114. [14] 江胜华,侯建国,何英明. 基于磁偶极子的磁场梯度张量局部缩并及试验验证[J]. 中国惯性技术学报,2017,25(4): 473-477.JIANG Shenghua, HOU Jianguo, HE Yingming, et al. Theoretical study and experimental verification of magnetic gradient tensor partial contraction using magnetic dipole[J]. Journal of Chinese Inertial Technology, 2017, 25(4): 473-477. [15] 江胜华,武立群,侯建国,等. 基于磁性标签石块的桥墩局部冲刷监测方法[J]. 重庆大学学报,2016,39(1): 88-97.JIANG Shenghua, WU Liqun, HOU Jianguo, et al. Bridge local scour monitoring using magnetic label rock[J]. Journal of Chongqing University, 2016, 39(1): 88-97. [16] 江胜华,周智,欧进萍. 基于磁测的边坡深部大变形监测方法[J]. 岩土力学,2013,34(10): 3033-3038.JIANG Shenghua, ZHOU Zhi, OU Jinping. Slope internal large deformation monitoring using magnetic survey[J]. Rock and Soil Mechanics, 2013, 34(10): 3033-3038. [17] 江胜华,周智,欧进萍. 基于磁场梯度定位的边坡变形监测原理[J]. 岩土工程学报,2012,34(10): 1944-1949.JIANG Shenghua, ZHOU Zhi, OU Jinping. Slope deformation monitoring principle based on magnetic gradient tensor[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(10): 1944-1949. [18] 干伟忠,金伟良,高明赞. 混凝土中钢筋加速锈蚀试验适用性研究[J]. 建筑结构学报,2011,32(2): 41-47.GAN Weizhong, JIN Weiliang, GAO Mingzan. Applicability study on accelerated corrosion methods of Steel bars in concrete structure[J]. Journal of Building Structures, 2011, 32(2): 41-47. [19] 张伟平, 王晓刚, 顾祥林等. 加速锈蚀与自然锈蚀钢筋混凝土梁受力性能比较分析[J]. 东南大学学报(自然科学版), 2006, 36(增刊Ⅱ): 139-144.ZHANG Weiping, WANG Xiaogang, GU Xianglin, et al. Comparative study on structural performance of reinforced concrete beams subjected to natural corrosion and accelerated corrosion[J]. Journal of Southeast University (Natural Science Edition), 2006, 36(SⅡ): 139-144. 期刊类型引用(6)
1. 袁国波,江胜华,何峻峰. 基于磁化强度的弹性阶段钢筋力-磁效应研究. 钢铁研究学报. 2025(05): 598-608 .  百度学术
百度学术2. 何峻峰,江胜华,孙伟贺,王廉强. 拉伸荷载作用下桥梁拉索钢丝/钢筋的力-磁效应研究. 材料导报. 2023(13): 219-226 .  百度学术
百度学术3. 李博阳,廖柯熹,何国玺,何腾蛟. 弱磁检测技术研究进展与展望. 电子测量与仪器学报. 2022(03): 1-14 .  百度学术
百度学术4. 江胜华,孙伟贺,王浩,刘晓春. 基于磁场梯度张量的斜拉桥拉索断丝监测方法. 长安大学学报(自然科学版). 2022(04): 52-62 .  百度学术
百度学术5. 江胜华,孙伟贺. 基于磁场梯度张量的拉索断丝监测方法. 农业工程学报. 2022(22): 141-148 .  百度学术
百度学术6. 张方,张开权,邓捷超,杨倩,韦翔,黄俊豪,龚婉婷,徐望喜,钱永久. 桥梁评估与加固2020年度研究进展. 土木与环境工程学报(中英文). 2021(S1): 152-166 .  百度学术
百度学术其他类型引用(2)
-





 下载:
下载:







 下载:
下载:
 百度学术
百度学术