Suppression Solutions to Transient Traction Current Interference in Neutral Zone for Track Circuit
-
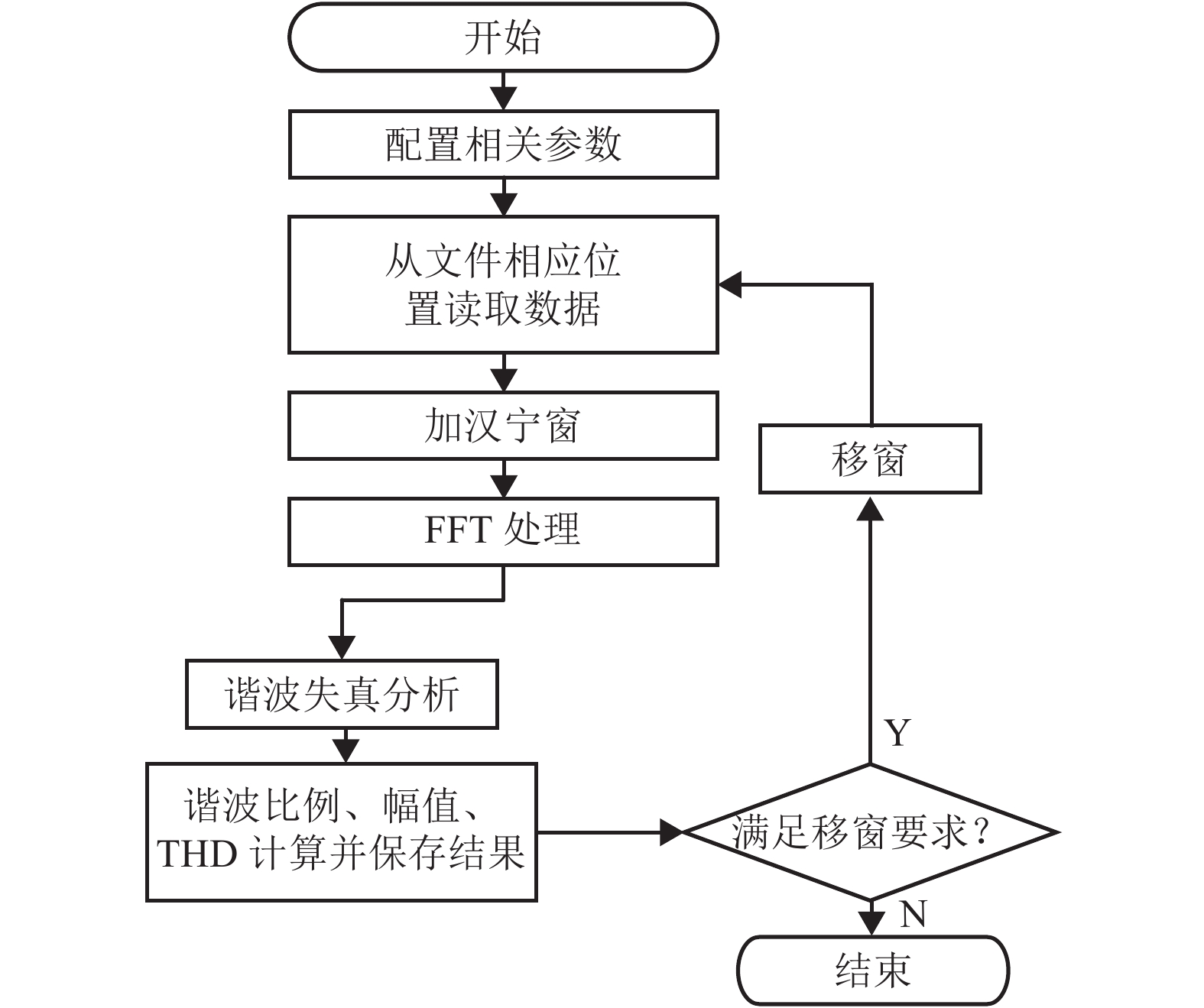
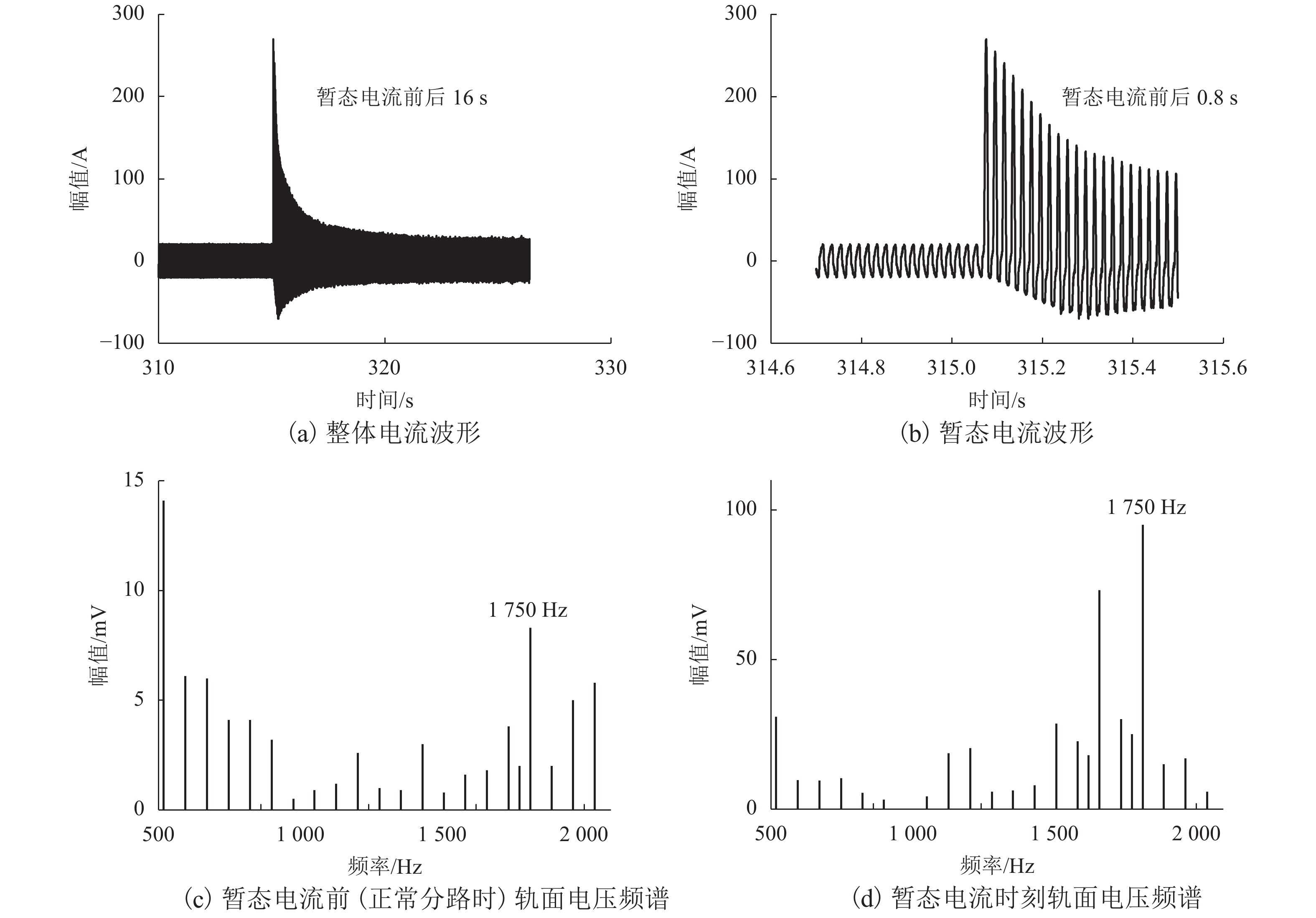
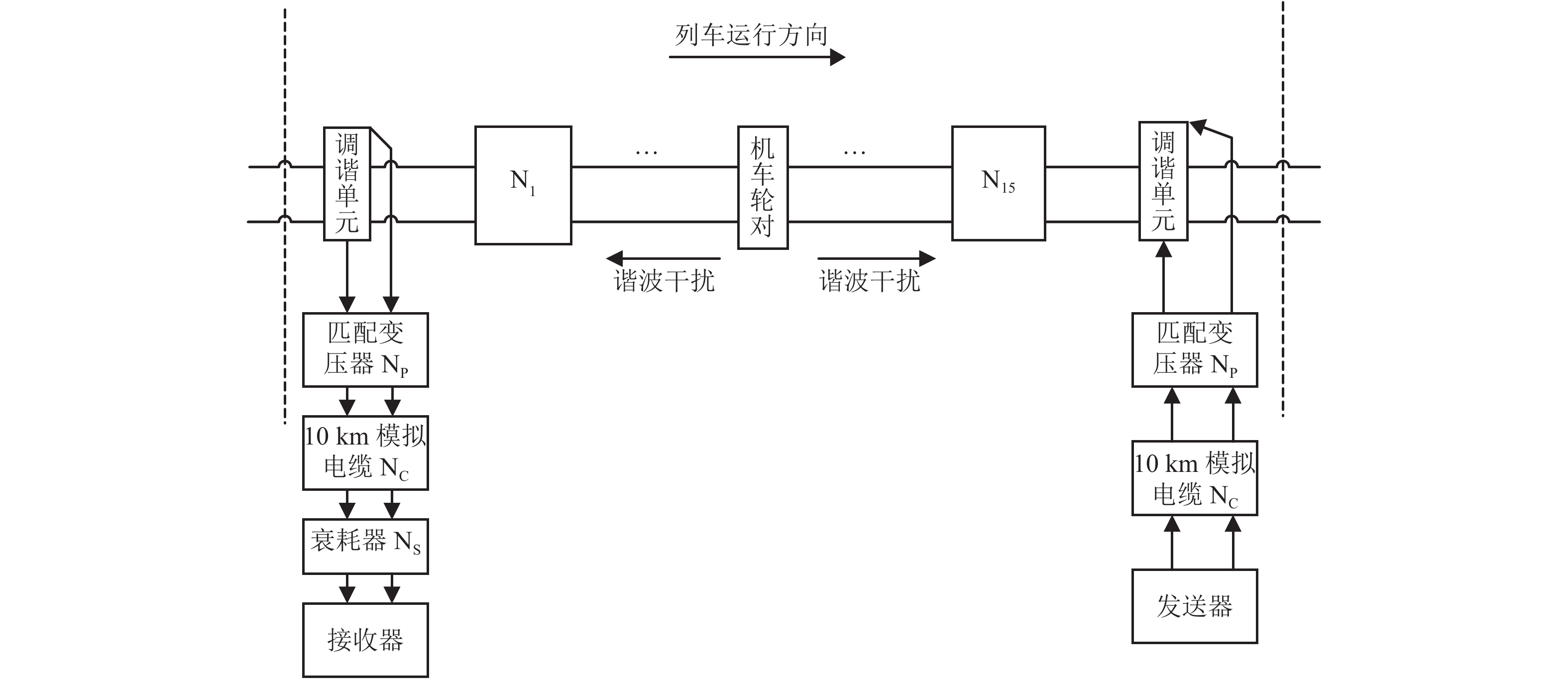
摘要: 电力机车及动车组经过含分相区的轨道区段时，暂态牵引电流中包含的谐波电流可能对轨道电路形成干扰并引发故障. 为保障轨道电路在谐波影响下可靠工作，对暂态电流干扰抑制方法进行了研究. 首先，按照欧标中加窗FFT （fast Fourier transformation）方法设计了谐波数据处理流程，给出现场测试数据分析结果，说明对轨道电路形成干扰的原因；然后，以信号载频1 700 Hz和谐波1 750 Hz为实例，从直接抑制谐波干扰的角度简要讨论了基于FPGA （field-programmable gate array）的FIR （finite impulse response）数字滤波器方案和仿真结果，并指出由于信号频带与谐波干扰非常接近，必然以较高阶数和处理延时作为代价；最后，基于谐波干扰的电流源特征和工程可行性，提出并重点阐述了轨道电路发送器和衰耗器的协同优化方案，通过合理配置发送器电平和衰耗器级数，在满足轨道电路调整、分路和机车信号状态的约束条件下，提高对谐波干扰的抑制效果，可将信号干扰比提高6 dB.Abstract: When an electric locomotive or an EMU (electric multiple unit) passes neutral zone in a track section, transient traction current is very likely to cause harmonic interference to track circuit, which may produce failure. To guarantee stable performance of track circuit under the influence of harmonic interference, the suppression methods of transient traction current are studied. Based on the European standards, the windowed FFT (fast Fourier transformation) method is adopted to design the procedure of harmonic data processing, and the analysis results of field test data are utilized to illustrate the interference mechanism for track circuit. Then, taking an example with a 1 700 Hz signal carrier and 1 750 Hz harmonic frequency, the solution and simulation results of FPGA (field-programmable gate array)-based FIR (finite impulse response) digital filter are briefly discussed from the point of direct suppression to harmonic interference. Due to the tiny difference between signal frequency and interference harmonic, the solution has to run at the cost of long response time and high order. Lastly, based on the current source feature of harmonic interference and project feasibility, the collaborative optimization scheme for the transmitter and attenuator of track circuit is proposed. Namely, by optimizing the transmitting level and attenuator step, the suppression to harmonic inference can be improved with an increase of 6 dB in signal-to-interference ratio while the operation states of track circuit are ensured including its clearance, occupancy and cab signaling.
-
五螺箍是一种新型组合式螺旋箍筋，其构造方式为中间一个大螺箍，四角为四个小螺箍. 相比传统的单螺箍圆形柱，四个小螺箍可以约束四个角落的混凝土，使得螺旋箍筋可以适用于矩形截面. 五螺箍为机械自动化生产，相对于传统箍筋有更高的效率[1]. 目前，五螺箍的应用与研究主要在中国台湾，且设计与研究参照了文献[2].
国内外学者对单螺箍约束混凝土开展了大量的理论与试验研究，而多螺箍约束混凝土的研究较少. Mohamed等[3]通过试验对复合箍筋柱进行了参数分析，主要研究了配箍形式和体积配箍率对试件力学性能的影响. Mander等[4]通过对大量约束混凝土柱试件进行轴心受压试验，得到一套约束混凝土的本构模型. Assa等[5-6]对一系列螺旋箍筋柱试件进行实验，得到螺旋箍筋约束混凝土的本构关系. 过镇海等[7-8]进行方形箍约束混凝土在反复荷载下的应力-应变全曲线试验研究，试验得出试件强度和延性与体积配箍率呈正相关关系. 唐琼等[9]基于多螺箍筋试验数据建立有限元模型，分析受力机理提出轴压承载力计算公式. 史庆轩等[10]通过多根不同配箍形式的方形截面柱进行轴压试验，并对其延性与强度进行影响因素分析. 翁正强等[11]对多个五螺箍短柱进行了轴压试验，研究了三个不同系列小螺箍直径对柱整体力学性能的影响. 郑亮[12]通过试验研究了方钢管混凝土和配螺旋箍筋方钢管混凝土短柱的力学性能，并且对短柱承载力计算方法进行理论研究. 傅明月[13]对五螺箍混凝土柱进行了轴心受压与偏心受压试验，发现螺旋箍筋能明显地提高柱的承载能力和延性性能. Liang等[14]进行9根足尺多螺旋箍筋约束方形短柱的试验，发现减小螺旋间距可以明显提高柱的轴压承载力和延性.
由于目前对五螺箍柱轴压承载力计算式的研究鲜有报道，因此，有必要对其力学性能进行进一步研究，以提出适用于五螺箍柱的轴压承载力计算式. 本文利用ABAQUS软件，首先，基于试验模型建立有限元模型，并将有限元分析结果与已有的试验结果进行对比分析，以验证有限元模型分析结果的准确性. 接着，基于材料用量相等的原则，创建4种不同配箍形式的矩形截面柱，并进行力学性能对比分析. 最后，对五螺箍柱轴压承载力进行影响因素分析，提出基于体积配箍率的轴压承载力计算式.
1. 有限元分析模型
1.1 混凝土的本构关系
混凝土本构模型采用有限元软件ABAQUS中内置的塑性损伤模型，损伤因子按文献[15]公式计算. 因Mander模型[14]对不同箍筋的作用形式有不同的计算式，故本构关系采用Mander模型[14]，模型的具体表达如下：
fcc=fcc1xrr−1+xr, (1) x=εcεcc, (2) εcc=εc0[1+5(fcc1fc0−1)], (3) r=EcEc−Esec, (4) Ec=5000√fcc, (5) Esec=fcc1εcc, (6) fcc1=fc0(−1.254+2.254√1+7.94f11fc0−2f11fc0), (7) f11=12Keρsfyh, (8) Ke=1−s2ds1−ρcc, (9) 式（1） ~ （9）中：
${f_{\text{cc}}}$ 为混凝土应力；$ {\varepsilon _{\text{c}}} $ 为混凝土应变；${f_{\text{cc1}}}$ 为约束混凝土的峰值应力；$ {\varepsilon _{{\text{cc}}}} $ 为约束混凝土的峰值应变；$ {f_{{\text{yh}}}} $ 为箍筋屈服强度；$ {s } $ 为箍筋间净间距；$ {d_{\text{s}}} $ 为约束箍筋的直径；$ {f_{{\text{c0}}}} $ 为混凝土轴心抗压强度标准值；$ {\varepsilon _{{\text{c0}}}} $ 为非约束混凝土的峰值应变，通常取0.002；$ {E_{\text{c}}} $ 为非约束混凝土弹性模型；${E_{{\text{sec}}}}$ 为约束混凝土割线模量；${f_{{{11}}}}$ 为侧向约束力，对于未约束混凝土${f_{11}}$ = 0；${K_{{\text{e}}}}$ 为有效约束系数；${\rho_{{\text{s}}}}$ 为体积配箍率；${\rho_{\text{cc}}}$ 为纵筋配筋率.1.2 采用的钢筋本构
钢筋采用理想弹塑性模型，具体表达形式为
{σs=Esεs,εs⩽εy,σs=Fy,εs>εy, (10) 式中：
${E_{{\text{s}}}}$ 、${F_{\text{y}}}$ 分别为钢筋的弹性模量和屈服强度；$ {\varepsilon _{\text{s}}} $ 为钢筋应变；$ {\varepsilon _{\text{y}}} $ 为钢筋屈服应变；$ {\sigma _{\text{s}}} $ 为钢筋应力.1.3 有限元模型验证
采用位移协调分离式来分析模型. 混凝土采用C3D8R单元，钢筋采用T3D2单元. 对钢筋和混凝土之间的连接，采用Embedded region进行两者的自由度耦合，不考虑钢筋和混凝土之间的连接滑移. 为了使柱体的边界约束条件接近实际受力情况，在柱体上、下两端采用铰接连接方式，并在柱顶进行位移加载. 本文选取文献[16]中的试件C2-1、C2-3、C2-4和C2-5，用有限元软件ABAQUS建模进行分析. 4根短柱的试验设计参数以及试验和有限元分析结果如表1所示. 图1为各试件试验和有限元分析的应力-应变曲线图.
表 1 试验和有限元计算结果对比Table 1. Comparison of experiment and finite element calculation results试件编号 材料强度/MPa 钢筋配置/mm 轴压承载力/kN 混凝土 纵筋 大螺箍 小螺箍 纵筋 大螺箍 小螺箍 试验值 模拟值 误差/% C2-1 39.4 420 280 280 D25 D13@50 D13@50 21670 22378 3.26 C2-3 40.3 D16@70 D13@70 20411 22109 8.32 C2-4 40.3 D13@60 D13@60 19336 21749 12.47 C2-5 39.4 D10@50 D10@50 18181 20128 10.70 从表1可以看出：轴压承载力的模拟结果稍微高于试验结果，轴压承载力最大误差为12.47%，最小误差为3.26%，平均误差仅为8.68%，可以说明有限元模拟得到的轴压承载力与试验结果比较接近. 从图1可以看出：有限元模拟结果和试验结果吻合较好.
2. 配箍形式对峰值荷载和延性的影响分析
基于材料用量相等的原则，考虑混凝土强度等级和配箍形式对钢筋混凝土柱受压性能的影响，设计了混凝土强度等级从C25 ~ C50的6组钢筋混凝土柱分析模型，每组都包括五螺箍、五环箍、矩形箍、矩形螺旋箍4种配箍形式，各配箍形式模型的几何参数和材料构成如图2所示. 为尽可能符合实际情况，柱高取1.5 m，即反弯点处截取一半楼层高度. 五螺箍、五环箍、矩形箍、矩形螺旋箍配箍形式的钢筋混凝土柱模型用钢量分别为1.10 × 107 、1.09 × 107 、 1.10 × 107、1.10 × 107 mm3，最大相差为0.5%，可视为材料用量相等. 4种配箍形式模型的纵筋配筋率为1.82%，满足轴心受压构件纵筋最小配筋率0.5%、最大配筋率5.0%的要求，箍筋强度均为280 MPa，纵筋强度均为400 MPa.
图 2 4种不同配箍形式矩形截面柱Figure 2. Four types of rectangular columns with different stirrup configurations有限元分析结果如图3、4所示. 从图3中可以看出：五螺箍柱的峰值承载力较其他3种柱都高. 为反映短柱的延性性能，采用已有的对延性定义的指标延性系数DI[17]来表示，如式（11）所示.
DI=u85/u11, (11) 式中：
$ {u_{11 }} $ 为峰值荷载时的位移；$ {u_{85 }} $ 为峰值荷载下降到85%时的位移.从图4可以看出：五螺箍的延性优于其他3种柱，五螺箍较五环箍、矩形箍和矩形螺旋箍柱构件峰值承载力均值分别提高0.78%、6.70%和13.73%，延性系数均值分别提高2.00%、10.32%和10.41%，表明五螺箍柱具有较优的承载力及延性，这与文献[11]中的试验结论相符.
由于五螺箍柱的各性能指标均较优，有必要对五螺箍轴压承载力及延性进行影响因素分析，为提出五螺箍轴压承载力的计算式奠定基础. 本文按照《混凝土结构设计规范》（GB 50010—2010）[18] （以下均简称《混规》）的要求，设计了9个螺旋箍筋间距为40 ~ 80 mm （或
${d_{{\text{cor}}}}/5$ ，其中，$ {d_{{\text{cor}}}} $ 为核心区混凝土的直径，可按螺旋箍筋内表面直径取值）的模型，其中，体积配箍率的计算式[11]为ρv=πDAsp1+4πdAsp2s5 Ach, (12) 式中：
$ D、d $ 分别为大螺箍和小螺箍的直径；$ {A}_{\text{sp1}}、 {A}_{\text{sp2}} $ 分别为大螺箍和小螺箍单根钢筋的截面面积；${A_{{\text{ch}}}}$ 为五螺箍所约束的混凝土面积；${s_{{\text{5 }}}}$ 为五螺箍的间距.有限元分析结果如图5和表2所示. 图5（a）中模型M-1、M-2、M-3分别对应的箍筋间距为45、50、55 mm，可以看出：随着箍筋间距的减小，五螺箍柱的峰值荷载和延性系数都有提高，曲线下降段也更为平缓，延性更好. 图5（b）中模型M-4、M-2、M-5分别对应的混凝土强度为23.4、26.8、29.6 MPa，可以看出：随着混凝土强度的提高，五螺箍柱的峰值荷载有明显的提高，但延性系数减小，延性不能得到改善. 图5（c）中模型M-2、M-6、M-7对应的箍筋强度分别为335、400、500 MPa，可以看出：提高螺旋箍筋的强度，五螺箍柱的峰值承载力和延性系数有所提高，主要表现为箍筋的约束应力提高，约束效果更好，下降段曲线也更为平缓，延性得到了较大改善. 图5（d）中模型M-2、M-8、M-9对应的大（小）螺箍直径分别为10（6）、10（8）、12（8） mm，可以看出：随螺旋箍筋截面直径的增大，峰值荷载和延性系数随之提升，曲线下降段也更为平缓，五螺箍柱的轴压承载力和延性都有很大改善. 对比图5（a）和图5（d），箍筋间距的减小和箍筋直径的增大都是提高体积配箍率的方式，对五螺箍柱的影响结果相似，均能提高构件的峰值承载力和延性，有利于提高构件在考虑近场地震[19]等不利作用下结构构件极限变形能力. 故下文将基于体积配箍率研究五螺箍柱的轴压承载力计算式.
表 2 有限元模型主要参数Table 2. Main parameters of finite element models编号 螺旋箍筋
间距/mm螺旋箍筋
强度/MPa混凝土
强度/MPa大（小）螺箍
直径/mm体积配箍率/% 峰值荷载/kN DI M-1 45 335 26.8 10(6) 2.15 11020.60 1.84 M-2 50 335 26.8 10(6) 1.93 10779.40 1.78 M-3 55 335 26.8 10(6) 1.76 10613.50 1.76 M-4 50 335 23.4 10(6) 1.93 9979.90 1.97 M-5 50 335 29.6 10(6) 1.93 11472.50 1.75 M-6 50 400 26.8 10(6) 1.93 11163.90 1.94 M-7 50 500 26.8 10(6) 1.93 11744.80 2.16 M-8 50 335 26.8 10(8) 2.45 11078.90 2.13 M-9 50 335 26.8 12(8) 3.01 11756.80 2.27 3. 轴压承载力计算
五螺箍柱的轴压承载力主要由以下4部分组成：混凝土抗压承载力、纵筋抗压承载力、大螺箍和小螺箍分别对核心区混凝土的约束效应而产生的承载力. 本文主要研究大、小螺箍通过对混凝土约束产生的承载力. 不同的配箍形式产生的约束效果不同，相对于矩形箍，圆形箍具有整体变形小，应力分布均匀及有效约束面积大等优点. 五螺箍柱中，大螺旋箍筋主要约束了柱中部的混凝土，小螺旋箍筋主要约束了柱四个角落的混凝土，二者相互弥补各自的弱约束区，较好地约束了整个截面. 螺旋箍筋有效约束区如图6所示，其中阴影部分表示有效约束区.
由于大、小螺箍的约束部位不同，故计算时应分别计算两者提供的约束作用力. 螺旋箍筋的有效约束面积[4]为
Ac=πd2cor4(1−s2dcor)2, (13) 式中：
$s$ 为螺旋箍筋的间距.《混规》[18]关于约束混凝土的轴心抗压强度为
fc*=fc+βσr， (14) 式中：
${\sigma _{\text{r}}}$ 为核心混凝土受到的径向压应力值，如式（15）；${f_{\text{c}}}$ 为混凝土抗压强度设计值；对于约束混凝土，取$\beta {\text{ = }}4$ .σr=2fyAsssdcor, (15) 式中：
${f_{\text{y}}}$ 为螺旋箍筋的抗拉屈服强度；${A_{{\text{ss}}}}$ 为单根螺旋箍筋的截面面积.在Hobbs[20]的研究中有
f∗c=fc+3.7(σrfc)0.86fc. (16) 根据叠加理论，基于《混规》[18]的五螺箍轴压承载力为
Nu1=0.9[fcAcor+8Ass1s1dcor1fy1Ac1+4×8Ass2S2dcor2fy2Ac2+fy3As1], (17) 式中：
${A_{{\text{ss1}}}}$ 和${A_{{\text{ss2}}}}$ 分别为单根大、小螺旋箍筋的截面面积；${f_{{\text{y1}}}}$ 和${f_{{\text{y2}}}}$ 分别为大、小螺旋箍筋的屈服强度；${s_{\text{1}}}$ 与${s_2}$ 分别为大、小螺旋箍筋的间距；${d_{{\text{cor1}}}}$ 和${d_{{\text{cor2}}}}$ 分别为大、小螺旋箍筋包围的核心区混凝土直径；${A_{{\text{cor}}}}$ 为混凝土核心区面积；${f_{\text{y3}}}$ 为纵筋抗压强度；${A_{\text{s1}}}$ 为纵筋面积；$ {A}_{\text{c1}}、{A}_{\text{c2}} $ 分别为大、小螺旋箍筋的有效约束面积.根据叠加理论，基于Hobbs[20]修正后的五螺箍轴压承载力为
Nu2=0.9[fcAcor+3.7fcAc1(2fy1Ass1s1dcor1fc)0.86+3.7fcAc2(2fy2Ass2s2dcor2fc)0.86×4+fy3As1]. (18) 文献[11]提出的五螺箍轴压承载力为
Nu3=0.85fc0Acc+fy3As1， (19) 式中：
${A_{{\text{cc}}}}$ 为五螺箍所约束的混凝土面积.美国ACI规范[2]规定的短柱受压承载力为
Nu4=0.85[0.85fc0(Ac−As1)+fy3As1]， (20) 式中：
${A_{\text{c}}}$ 为混凝土柱全断面积；方括号外的“0.85”表示结构抗力折减系数，方括号内的“0.85”表示尺寸效应对受压承载力的影响系数.由上文轴压承载力影响因素分析可知，材料的强度、箍筋的间距、箍筋的面积等都对五螺箍柱的承载力有影响，为简便起见，本文将这些因素统一考虑为体积配箍率
${\rho _{\text{v}}}$ ，这样就可以很大程度上减小承载力计算的复杂程度. 由于混凝土及纵筋所提供的竖向承载力计算较为明确，无需修正，本文重点修正螺旋箍筋对混凝土的约束作用. 将每个构件的轴压承载力减去混凝土和纵筋提供的竖向承载力，得到螺旋箍筋提供的竖向承载力${N}_{1}$ ，由此可以推出约束作用系数为ξ=N1/[fcfy(Ac1+4Ac2)]. (21) $\xi $ 随${\rho _{\text{v}}}$ 的变化关系如图7所示，对两者进行线性关系拟合，结果可以看出两者大致成线性分布. 根据$\xi $ 与${\rho _{\text{v}}}$ 的关系，参考《混规》[18]和Hobbs[20]修正按叠加理论计算的公式，本文提出五螺箍柱的轴压承载力为
图 7 约束作用系数-体积配箍率关系Figure 7. Relationship between confinement coefficients and volume-stirrup ratiosNu5=0.9[fcAcor+fy3As1+fcfy(Ac1+4Ac2)(0.0019+0.076ρv)]. (22) 采用上述5个承载力计算式（即式（17）~（20）和式（22）），不考虑安全储备及折减系数，混凝土强度统一采用轴心抗压强度标准值，得到上述9个模型和4个试验[16]构件的轴压承载力，分别如表3和表4所示. 表中：
${\delta _{\text{1}}}$ 、$ {\delta _{\text{2}}} $ 、${\delta _{\text{3}}}$ 、${\delta _{\text{4}}}$ 和${\delta _{\text{5}}}$ 为5个承载力对应的相对误差.表 3 9个模型的轴压承载力计算Table 3. Axial compression bearing capacity calculation of nine models编号 模拟值 Nue/kN 计算值/kN 相对误差/% ${N_{{\text{u1}}}}$ ${N_{{\text{u2}}}}$ ${N_{{\text{u3}}}}$ ${N_{{\text{u4}}}}$ ${N_{{\text{u5}}}}$ ${\delta _{\text{1}}}$ $ {\delta _{\text{2}}} $ ${\delta _{\text{3}}}$ ${\delta _{\text{4}}}$ ${\delta _{\text{5}}}$ M-1 11020.60 10024.25 10459.24 6543.56 7871.88 11039.23 −9.04 −5.09 −40.62 −28.57 0.17 M-2 10779.40 9601.01 10019.12 6543.56 7871.88 10675.10 −10.93 −7.05 −39.30 −26.97 −0.97 M-3 10613.50 9258.53 9656.58 6543.56 7871.88 10373.72 −12.77 −9.02 −38.35 −25.83 −2.26 M-4 9979.90 9001.25 9362.72 6002.76 7162.57 9610.15 −9.81 −6.18 −39.85 −28.23 −3.70 M-5 11472.50 10094.93 10555.22 6988.93 8456.03 11552.11 −12.01 −8.00 −39.08 −26.29 0.69 M-6 11163.90 10104.07 10515.16 6543.56 7871.88 11386.56 −9.49 −5.81 −41.39 −29.49 1.99 M-7 11744.80 10878.01 11257.04 6543.56 7871.88 12481.12 −7.38 −4.15 −44.29 −32.98 6.27 M-8 11078.90 10056.88 10453.68 6543.56 7871.88 11110.52 −9.22 −5.64 −40.94 −28.95 0.29 M-9 11756.80 10962.58 11334.17 6543.56 7871.88 11579.44 −6.76 −3.59 −44.34 −33.04 −1.51 绝对值均值 9.71 6.06 40.91 28.93 1.98 标准差 0.0197 0.0175 0.0215 0.0261 0.0195 由表3数据可知：计算值
${N_{{\text{u3}}}}$ 远远小于模拟值和试验值，原因是该式中混凝土的计算面积是五螺箍约束混凝土的面积，且混凝土抗压强度取的是轴心抗压强度标准值，而不是约束后的混凝土抗压强度值；计算值${N_{{\text{u4}}}}$ 相比模拟值和试验值误差较大，原因是计算式仅考虑了纵筋和混凝土提供的竖向抗压承载力，而忽略了螺旋箍筋对混凝土的约束作用；计算值${N_{{\text{u1}}}}$ 和${N_{{\text{u2}}}}$ 比较接近模拟值和试验值，两个计算式既考虑了混凝土和纵筋所提供的竖向抗压承载力，又考虑了箍筋对混凝土的约束效应；在分析范围内，本文提出的修正式的计算值${N_{{\text{u5}}}}$ 更加接近模拟值和试验值，与模拟值的误差均值为1.98%，与试验值的误差均值为2.83%，且标准差分别为0.0195和0.0216，总体上偏于安全. 用体积配箍率考虑箍筋的间距、箍筋的面积、螺箍直径等多因素使得承载力计算更加简便与精确，且具有很好的实用性.表 4 4个试验构件的轴压承载力Table 4. Axial compression bearing capacity calculation of four test members编号 试验值[16]/kN 计算值/kN 相对误差/% ${N_{{\text{u1}}}} $ ${N_{{\text{u2}}}} $ ${N_{{\text{u3}}}} $ ${N_{{\text{u4}}}} $ ${N_{{\text{u5}}}} $ ${\delta _{\text{1}}} $ ${\delta _{\text{2}}} $ ${\delta _{\text{3}}} $ ${\delta _{\text{4}}} $ ${\delta _{\text{5}}} $ C2-1 21672.00 20569.22 21094.45 12090.38 11518.40 22156.09 −5.09 −2.66 −44.21 −46.85 2.23 C2-2 20412.00 19005.14 19508.17 12291.21 11706.16 20390.35 −6.89 −4.43 −39.78 −42.65 −0.11 C2-4 19332.00 19334.76 19871.39 12291.21 11706.16 20319.01 0.01 2.79 −36.42 −39.45 5.11 C2-5 18181.00 17305.58 17781.27 12090.38 11518.40 18883.65 −4.82 −2.20 −33.50 −36.65 3.86 绝对值均值 4.20 3.02 38.48 41.40 2.83 标准差 0.029 4 0.009 7 0.046 0 0.043 9 0.021 6 4. 结 论
1） 建立与参考文献中试验模型一致的五螺箍短柱有限元模型进行对比分析，分析结果显示有限元模拟结果与试验结果误差较小，在可接受范围内，从而验证了该有限元模型的正确性.
2） 基于材料用量相等原则，对4种不同配箍形式的短柱进行对比分析，表明五螺箍柱承载力和延性均较优.
3） 对五螺箍柱进行影响因素分析，改变材料强度、螺箍间距、箍筋面积等均能改变五螺箍柱性能，提高配箍率可以明显改善五螺箍柱的延性及峰值承载力.
4） 在多个参数分析的基础上，提出了基于体积配箍率的五螺箍短柱轴压承载力计算方法，与各国规范式对比，该式更为简便且较为精确.
-
图 1 加窗FFT处理谐波数据流程
Figure 1. Flowchart of harmonic data processing by utilizing windowed FFT
图 2 列车过分相区钢轨电流波形与轨面电压频谱
Figure 2. Waveform of rail current and spectrum of rail surface voltage when a train passes neutral zone
图 3 轨道电路抑制谐波干扰示意
Figure 3. Sketch of suppressing harmonic interference to track circuit
表 1 暂态谐波电流及比例
Table 1. Transient harmonic current and its proportion
谐波频率/Hz 电流/A 比例/% 谐波频率/Hz 电流/A 比例/% 1 550 0.149 0.31 1 800 0.040 0.09 1 600 0.085 0.18 1 850 0.058 0.13 1 650 0.128 0.28 1 900 0.100 0.22 1 700 0.063 0.16 1 950 0.149 0.31 1 750 0.295 0.61 2 000 0.048 0.10 
下载: 导出CSV
表 2 谐波1 750 Hz时测试数据
Table 2. Filed test data in the case of 1 750 Hz harmonic
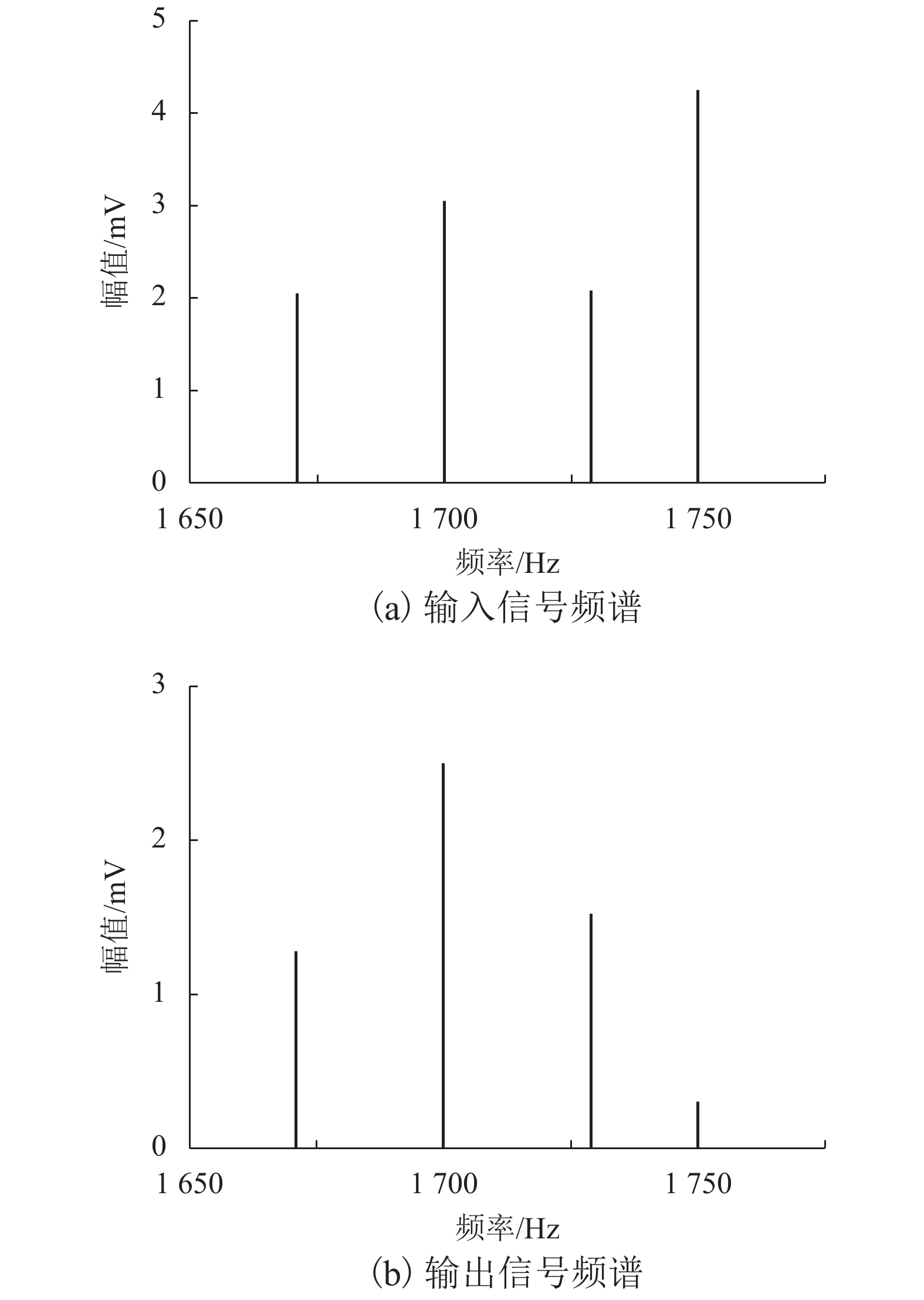
序号 钢轨 1 电流/A 钢轨 2 电流/A 总电流/A 不平衡度/% 轨面电压/V 视入阻抗/Ω 1 0.425 0.347 0.772 10.01 0.090 1.159 2 0.426 0.347 0.773 10.12 0.048 0.611 3 0.386 0.309 0.695 11.12 0.102 1.313 4 0.463 0.386 0.849 9.09 0.157 2.032 5 0.579 0.463 1.043 11.12 0.143 1.231
下载: 导出CSV
表 3 数字滤波器衰减特性
Table 3. Attenuation characteristics of digital filter
项目 频率
/Hz滤波前电压
/mV滤波后电压
/mV相对增益
/dB谐波 1 750 4.25 0.30 信号 1 671 2.05 1.28 18.93 1 700 3.05 2.50 21.29 1 729 2.08 1.52 20.30
下载: 导出CSV
表 4 某故障区段发送器电平等级表
Table 4. Transmission voltage levels used in a fault section
等级编号 1 2 3 4 5 电平/V 142.0 126.0 111.0 95.0 79.2 等级编号 6 7 8 9 电平/V 62.8 47.3 31.8 15.8
下载: 导出CSV
表 5 不同电平等级对应衰耗参数
Table 5. Attenuation values for different voltage levels
参数 电平等级 1 2 3 4 发送器电压/V 142 126 111 95 衰耗参数范围 116∶（25～50） 116∶（28～53） 116∶（31～56） 116∶（37～60） SIR/dB 17.84～17.98 16.95～17.10 16.03～16.18 14.93～15.08 SIR均值/dB 17.90 17.01 16.10 15.00
下载: 导出CSV
表 6 不同电平等级下优化组合仿真数据
Table 6. Simulation data of optimization strategy under different voltage levels
项目 参数 电平等级 1 1 4 5 参数取值 发送器电压/V 142 142 95 79.2 衰耗级数 116:25 116:50 116:37 116:43 轨面干扰电压/V 0.095 0.095 0.095 0.095 分路状态 接收信号残压/V 0.033 6 0.067 0 0.033 4 0.032 7 接收干扰残压/V 0.031 9 0.062 8 0.044 2 0.061 6 接收器残压/V 0.068 6 0.137 2 0.086 9 0.094 3 机车信号 短路电流/A 1.016 3 1.016 3 0.679 9 0.566 9 接收电压/V 0.797 1 0.797 1 0.533 3 0.444 6 衰减 干扰/dB 9.48 3.60 6.65 信号/dB −0.24 −6.23 −0.18 调整状态 接收信号电压/V 0.248 9 0.497 7 0.246 4 0.238 7 接收干扰电压/V 0.031 9 0.062 8 0.044 2 0.061 6 调整SIR/dB 17.84 17.98 14.93 11.76
下载: 导出CSV
-
YANG Shiwu, TIAN Jianzhao, XU Hao, et al. Analysis on harmonic current and its impact on track circuit in high speed railway[C]//2016 IEEE International Conference on Intelligent Rail Transportation. Birmingham: IEEE, 2016: 315-321. YANG Shiwu, ZHU Bei, CLIVE Roberts, et al. Feature-based solution to harmonics interference on track circuit in electrified heavy haul railway[C]//2013 IEEE International Conference on Intelligent Rail Transportation. Beijing: IEEE, 2013: 297-301. 李彩霞,杨世武,张炜. 轨道电路不平衡牵引电流干扰测试及分析[J]. 铁道通信信号,2009,45(7): 25-26. doi: 10.3969/j.issn.1000-7458.2009.07.012LI Caixia, YANG Shiwu, ZHANG Wei. Test and analysis of non-balance electric current interfere in track circuit[J]. Railway Signalling & Communication, 2009, 45(7): 25-26. doi: 10.3969/j.issn.1000-7458.2009.07.012 LI Jianqing, YANG Shiwu, REN Guoqiao. Research on anti-interference from heavy traction current to the signaling system of Datong-Qinhuangdao railway line[C]//Proceedings of 9th International Heavy Haul Conference. Shanghai: China Railway Publishing House, 2009: 734-748. British Standard Institution. Railway applications-compatibility between rolling stock and train detection systems-part2: compatibility with track circuits: CLC/TS50238-2.2015[S]. London: British Standards Institution, 2015. 中华人民共和国铁道部. 铁道信号电气设备电磁兼容性试验及其限值: TB/T 3073[S]. 北京: 中国铁道出版社, 2003. ŽUPAN A, TEKLIC A T, FILIPOVIC-GRCIC B. Modeling of 25 kV electric railway system for power quality studies[C]//IEEE EUROCON Conference. Zagreb: IEEE, 2013: 844-849. FATEN O, BEN AMMAR F. Compensation of harmonic disturbances in the tunisian SAHEL railway supply system[C]//1st International Conference on Electrical Engineering and Software Applications. Hammamet: IEEE, 2013: 574-578. JIAO Jinghai, WEN Yinghong, LI Meng, et al. Research on vehicle onboard measurement system of traction harmonic current for analyzing interference on track circuit[C]//6th IEEE International Symposium on Microwave, Antenna, Propagation, and EMC Technologies. Shanghai: IEEE, 2015: 475-478. 王梓丞,郭进,张亚东,等. 基于FDTD接口方法的ZPW-2000轨道电路暂态分析[J]. 西南交通大学学报,2019,54(1): 196-201, 218. doi: 10.3969/j.issn.1673-4440.2016.04.024WANG Zicheng, GUO Jin, ZHANG Yadong, et al. Transient analysis of ZPW-2000 track circuit based on FDTD interface method[J]. Journal of Southwest Jiaotong University, 2019, 54(1): 196-201, 218. doi: 10.3969/j.issn.1673-4440.2016.04.024 许童羽,程浩忠,周玉宏,等. 基于LabVIEW的配电网谐波在线监测与分析系统[J]. 电力系统保护与控制,2008,36(1): 63-66. doi: 10.3969/j.issn.1674-3415.2008.01.014XU Tongyu, CHENG Haozhong, ZHOU Yuhong, et al. A LabVIEW-based system for distribution network harmonics monitoring and analysing[J]. Power System Protection and Control, 2008, 36(1): 63-66. doi: 10.3969/j.issn.1674-3415.2008.01.014 英超. 基于加窗插值FFT的电力系统谐波检测算法研究[D]. 锦州: 辽宁工业大学, 2015. PHAM V L, WONG K P. Wavelet-transform-based algorithm for harmonic analysis of power system waveforms[J]. IEEE Proceedings-Generation,Transmission and Distribution, 1999, 146(3): 249-254. doi: 10.1049/ip-gtd:19990316 毛广智,解学书. 无绝缘轨道电路系统的图形建模[J]. 计算机工程,2004,30(15): 146-148. doi: 10.3969/j.issn.1000-3428.2004.15.058MAO Guangzhi, XIE Xueshu. Graphic modeling of jointless track circuit[J]. Computer Engineering, 2004, 30(15): 146-148. doi: 10.3969/j.issn.1000-3428.2004.15.058 RUDEZ U, MIHALIC R. Sympathetic inrush current phenomenon with loaded transformers[J]. Electric Power Systems Research, 2016, 138: 3-10. doi: 10.1016/j.jpgr.2015.12.011 何垚. 高速铁路车网谐波特性研究[D]. 成都: 西南交通大学, 2013. HOBBS I. High speed power[J]. Power Engineering, 2007, 21(2): 32-35. doi: 10.1049/pe:20070204 杨少兵,吴命利. 基于实测数据的高速动车组谐波分布特性与概率模型研究[J]. 铁道学报,2010,32(3): 33-38. doi: 10.3969/j.issn.1001-8360.2010.03.006YANG Shaobing. WU Mingli. Study on harmonic distribution characteristics and probability model of high speed emu based on measured data[J]. Journal of the China Railway Society, 2010, 32(3): 33-38. doi: 10.3969/j.issn.1001-8360.2010.03.006 王纪坤. ZPW-2000R移频自动闭塞系统测试系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. 张海洋,许海平,方程,等. 基于谐振数字滤波器的直驱式永磁同步电机转矩脉动抑制方法[J]. 中国电机工程学报,2018,38(4): 1222-1231,1299.ZHANG Haiyang, XU Haiping, FANG Cheng, et al. Torque ripple suppression method of direct-drive permanent magnet synchronous motor based on resonant digital filter[J]. Proceedings of the CSEE, 2018, 38(4): 1222-1231,1299. 杨世武. 铁路信号电磁兼容技术[M]. 北京: 中国铁道出版社, 2010: 80-86. 中华人民共和国铁道部. 铁路信号维护规则技术标准I[M]. 2版. 北京: 中国铁道出版社, 2008: 92-93 刘家良. 移频轨道电路邻线干扰与迂回电路研究[D]. 北京: 北京交通大学, 2015. 期刊类型引用(4)
1. 龚书锦，陈志忠. 降低站内无轨道电路区段不平衡牵引电流干扰问题探讨. 铁路通信信号工程技术. 2023(S1): 18-22 . 
百度学术2. 唐伟，史籍. 牵引回流对ZPW-2000A轨道电路的影响及解决措施. 铁路通信信号工程技术. 2022(S1): 122-126 . 百度学术3. 董昱，魏万鹏. 基于RBF神经网络PID控制的列车ATO系统优化. 电子测量与仪器学报. 2021(01): 103-109 . 百度学术4. 田粉霞，杨世武，崔勇，武沛. 基于改进卷积神经网络的无绝缘轨道电路调谐区故障诊断. 铁路计算机应用. 2020(06): 58-63+74 . 百度学术其他类型引用(7)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 526
- HTML全文浏览量: 252
- PDF下载量: 20
- 被引次数: 11