Fault Diagnosis of Rolling Bearing Based on EEMD-Hilbert and FWA-SVM
-
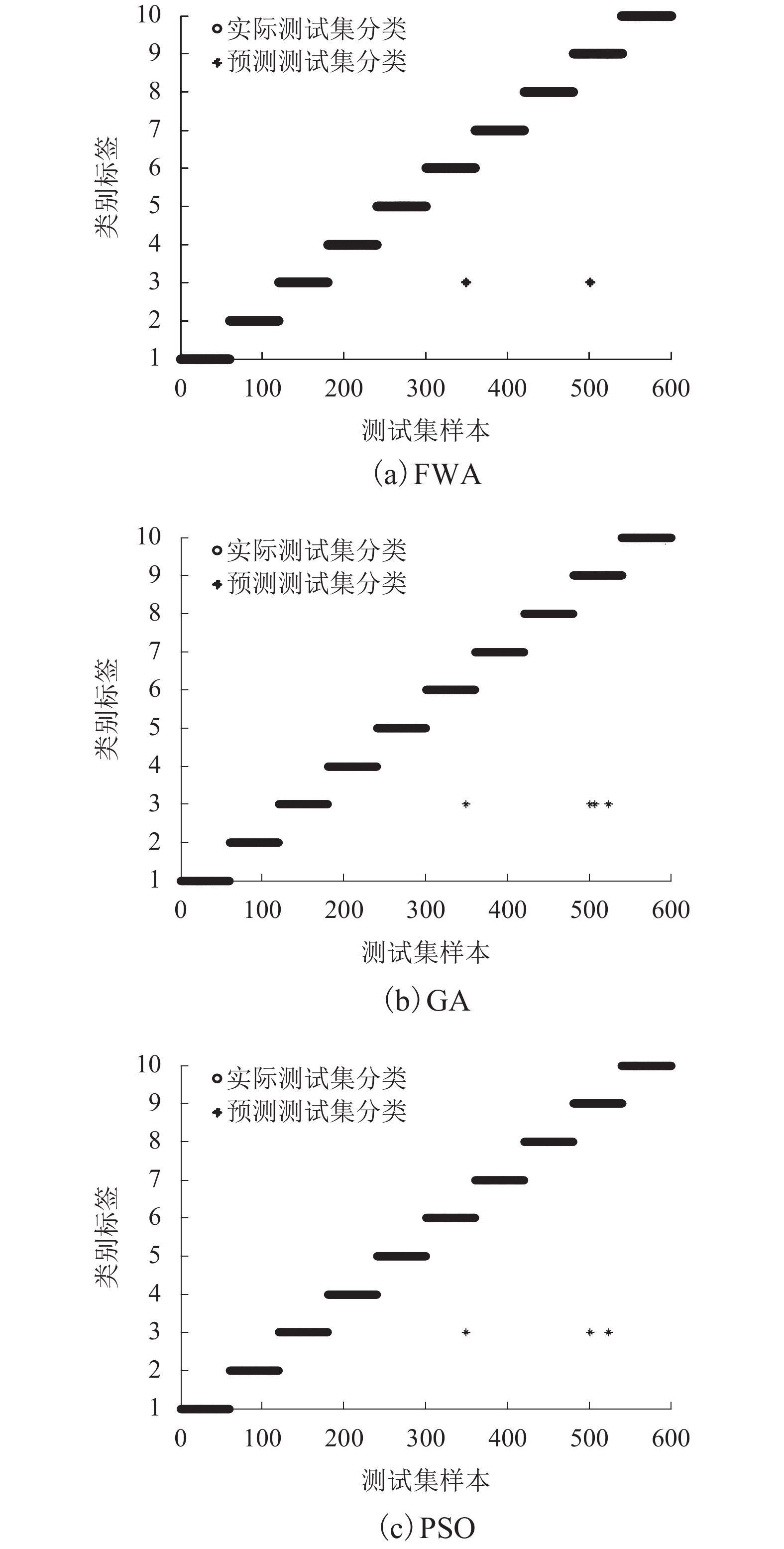
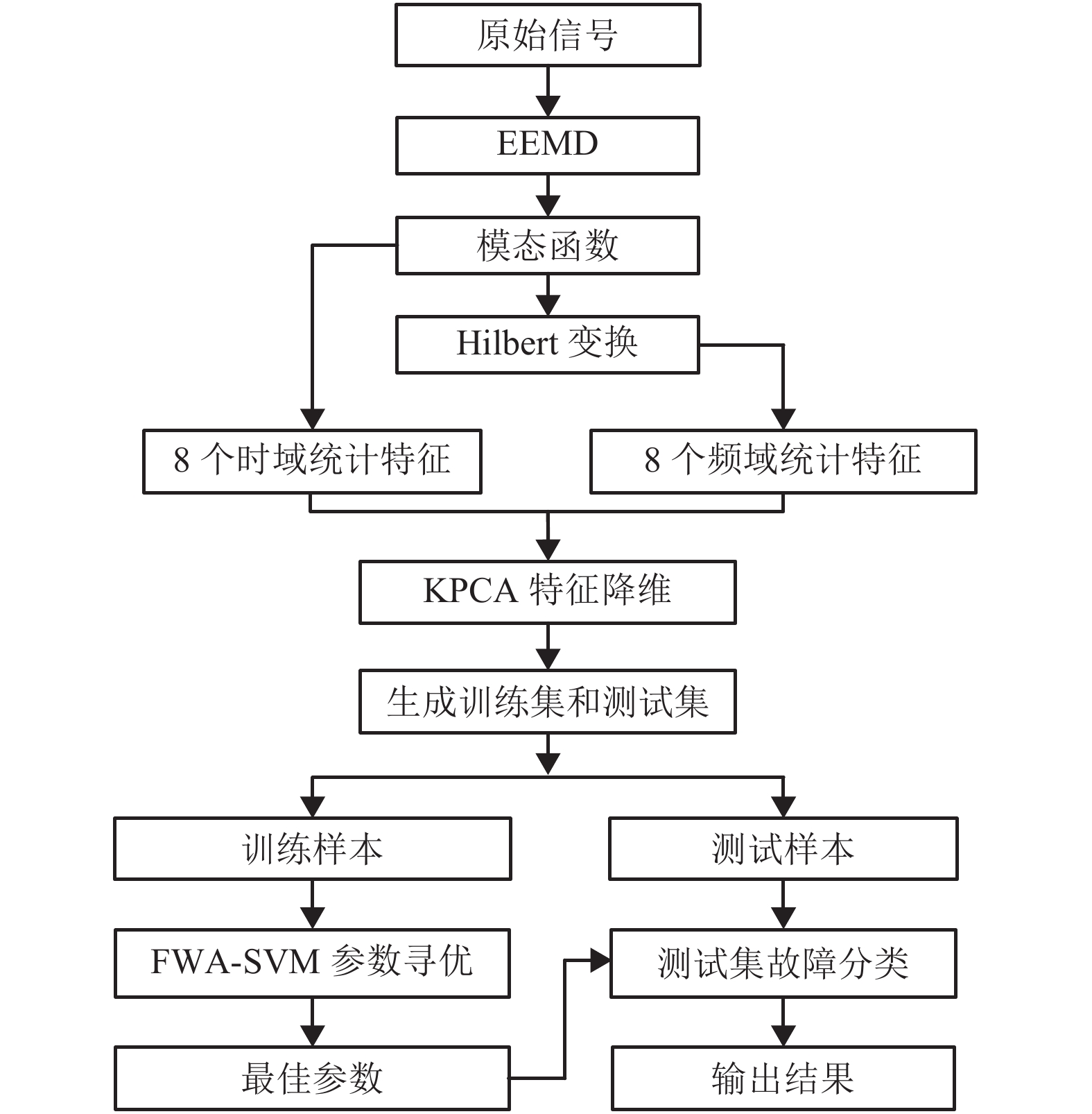
摘要: 为有效提取非平稳特性的滚动轴承振动信号特征,提高故障诊断效率,提出一种采用集合经验模态分解(empiricalmode decomposition,EEMD)、Hilbert变换的特征提取方法,并利用烟花算法优化支持向量机(support vector machine,SVM)分类参数的滚动轴承故障诊断方法. 通过EEMD方法将目标信号分解成若干个模态函数,采取Hilbert变换获取模态函数的瞬时频率,并对模态函数及其瞬时频率进行统计特征提取,从而实现特征的有效降维. 结果表明:信号经过EEMD-Hilbert处理后特征能有效提取,将训练集和测试集各600组数据代入烟花算法优化SVM模型得到测试集正确率为99.63%;比传统的遗传算法和粒子群算法优化模型分别提高0.4%和0.2%左右;同时收敛时间更短,验证了该算法模型的可行性与有效性.Abstract: To effectively extract the non-stationary characteristics of the rolling bearing vibration signal and improve the fault diagnosis efficiency, a feature extraction method based on the ensemble empirical mode decomposition (EEMD) and Hilbert transform was proposed. The support vector machine (SVM) classification parameters were optimised using the fireworks algorithm (FWA) for the rolling bearing fault diagnosis method. The EEMD method was used to decompose the target signal into several modal functions. The instantaneous frequencies of the modal functions were obtained through Hilbert transforms. Statistical feature extraction and dimensionality reduction were respectively performed for the modal function and instantaneous frequency. The fireworks algorithm model was used to optimise the SVM parameters as well as the multi-classification fault diagnosis with training and test sets drawn from 600 datasets. The accuracy of the signal is estimated to be 99.633%, which is 0.4% and 0.2% higher than that of the traditional genetic algorithm and particle swarm optimisation algorithm, respectively. Further, the ability of iterative convergence is also seen to have obvious advantages. The feasibility and validity of the algorithm models are thus verified.
-
磁悬浮技术具有无摩擦、微振动、长寿命及高精度等优点,被广泛地应用于高速机械领域. 磁轴承作为核心部件,一般与高速旋转电机配合用于高速旋转机械,如磁悬浮飞轮、磁悬浮控制力矩陀螺及磁悬浮电机等[1-3]. 对于直线运动,通常采用能够实现悬浮及导向功能的电磁铁与直线电机的组合,如磁浮列车、磁浮电梯等. 目前为止,世界很多国家已经对磁浮列车技术研究了较长时间,而且部分实现了商业运行,如中国、德国、日本、韩国等[4-6]. 磁浮列车由电磁铁与轨道功能件之间产生的电磁力支撑,从而实现无接触运行. 电磁铁为悬浮系统的核心执行部件,其电磁力特性决定了列车的承载能力,并与控制器、传感器相互配合实现列车的稳定悬浮. 尤其对于高速运行的磁浮列车,运行载荷更加复杂、苛刻,对承载能力及稳定性要求更高. 因此,电磁力特性分析作为基础研究,对悬浮系统的设计及优化起至关重要作用[7-9].
目前,电磁力建模分析方法主要包含等效磁路法(EMC)及有限元法(FEM),其中,FEM计算精度较高,但效率较低,很难与控制模型联合用于分析系统实时特性. EMC计算速度较高,能够与控制模型联合用于系统实时动态特性分析,但其计算精度较低. 因此,在传统EMC模型中通常会考虑加入补偿系数,通过调整系数校正电磁力结果,使其与FEM结果接近[10-11]. 然而,传统EMC模型仅考虑线性工作区,导磁材料采用恒定的相对磁导率,忽略磁饱和影响,甚至忽略导磁材料磁阻. 这样会导致EMC模型结果在小电流区间内较准确,而在大电流区间就会出现较大偏差[12-13]. 本文在搭建高速磁浮悬浮电磁铁EMC模型时,考虑了导磁材料的磁阻及其非线性. 通过导磁材料B-H (B为磁感应强度;H为磁场强度)曲线的拟合及引入,求解电磁力的准确性大幅度提高,适用范围增加.
高速磁浮列车的悬浮电磁铁共有12个磁极,极性为NS交替,相邻磁极之间通过磁轭连接,磁场经过长定子铁芯形成回路,磁极与长定子之间的磁场产生电磁吸力,实现悬浮功能. 12个磁极分为左、右两组,分别由两个悬浮控制器单独控制,从而形成两个控制回路,每个回路对应两个间隙传感器. 传感器实时监测电磁铁与长定子之间的间隙,并反馈给悬浮控制器,经过控制策略计算,悬浮控制器输出相应电压给悬浮电磁铁,实现动态稳定悬浮.
1. 电磁铁模型搭建
1.1 等效磁路
悬浮电磁铁与长定子的物理模型如图1所示. 其中电磁铁分为左、右两个回路单独控制,为简化计算模型,仅对半个电磁铁进行建模,并忽略两个回路间磁场的影响. 搭建的等效磁路模型如图2所示,磁路中包含了气隙磁阻、漏磁磁阻及导磁材料磁阻. 图中:Raj为磁极与长定子间的气隙磁阻;Rsi为长定子铁芯磁阻;Rei为磁极铁芯及磁轭磁阻;Rli为相邻磁极之间的漏磁磁阻;ϕaj、ϕsi、ϕei及ϕli分别为磁阻Raj、Rsi、Rei及Rli对应的磁通;ϕpj 为磁极磁通;θj为磁极磁动势nI,n为磁极匝数,I为控制回路电流;i=1,2,…,5,j=1,2,…,6.
根据建模需求,定义磁通、磁动势向量为
{ϕ=(ϕ1,ϕl1,ϕ2,ϕl2,⋯,ϕ5,ϕl5)T,ϕs=(ϕ1,ϕ2,⋯,ϕ5)T,ϕa=(ϕ1,ϕ1+ϕ2,⋯,ϕ4+ϕ5,ϕ5)T,ϕe=(ϕ1+ϕl1,ϕ2+ϕl2,⋯,ϕ5+ϕl5)T,ϕp=(ϕ1+ϕl1,ϕ1+ϕl1+ϕ2+ϕl2,⋯,ϕ4+ϕl4+ϕ5+ϕl5,ϕ5+ϕl5)T,θ=(θ1,θ2,⋯,θ6)T. (1) 磁极磁通向量ϕp与磁通向量ϕ的转换关系为
ϕp =Tϕ,
式中:
T=[11111111111111111111]. 在等效磁路中,根据基尔霍夫电压定律,建立关于磁通的方程组,如式(3).
{Ra(j−1)ϕa(j−1)+Rsiϕsi+Rajϕaj+Reiϕei=θj−1+θj,Rliϕli+Reiϕei=θj−1+θj, (3) 式中:j=2,3,⋯,6.
将式(1)表达为矩阵及向量形式为
Aϕ=TTθ=TTnI, (4) 式中:向量n=(n, n, n, n, n, n)T;A为磁阻矩阵,A∈R10×10,
A=[Ra1+Ra2+Rs1+Re1Re1Ra200⋯Re1Rl1+Re1000⋯Ra20Ra2+Ra3+Rs2+Re2Re2Ra3⋯00Re2Rl2+Re20⋯⋮⋮⋮⋮⋮]. 1.2 磁阻计算
1) 磁极与长定子间气隙磁阻
受磁极直线发电机(linear generator, LIG)槽与长定子齿槽结构的影响,磁极与长定子之间的气隙磁通分布较为复杂,如图3所示. 因此,将气隙磁通等效分为主磁通、槽磁通及LIG磁通,分别对应3种磁阻.
气隙磁阻为3种磁阻并联,即
1Raj=1Ra,mj+1Ra,nj+1Ra,Lj, (5) 式中:Ra,mj为主磁通对应的磁阻;Ra,nj为槽磁通对应的磁阻;Ra,Lj为LIG磁通对应的磁阻.
每种磁阻可由式(6)计算.
Ra,oj=sj+hojμ0Aa,oj,o∈[m,n,L], (6) 式中:sj为磁极与长定子齿之间的间隙;μ0为空气磁导率;Aa,oj为相应气隙面积;hoj为额外气隙长度;m、n、L分别对应主磁通、槽磁通和LIG磁通.
2) 相邻磁极间漏磁磁阻
磁极磁通大部分经过长定子回到相邻磁极,小部分未经过长定子而直接回到相邻磁极,该部分磁通为相邻磁极之间的漏磁,对应的磁阻称为漏磁磁阻,可由式(7)计算.
Rli=hliμ0Ali, (7) 式中:Ali为等效气隙面积;hli为相邻磁极间的等效气隙长度.
3) 导磁材料磁阻
对于长定子铁芯、磁极铁芯及磁轭的磁阻,采用分段方式进行求解,且尽可能保证每段的截面积相同. 具体分段如图4所示,其中,磁极及磁轭共分为5段(1~5),长定子分为3段(6~8). 该部分磁阻计算时考虑导磁材料的非线性.
磁极铁芯及磁轭磁阻为
Rei=5∑k=1lei,kμ0μr(ϕei,k)Aei,k; (8) 长定子铁芯磁阻为
Rsi=8∑k=6lsi,kμ0μr(ϕsi,k)Asi,k, (9) 式(8)、(9)中:lei,k, lsi,k分别为悬浮电磁铁侧、长定子侧每段铁芯的长度;Aei,k, Asi,k分别
为悬浮电磁铁侧、长定子侧每段铁芯的截面积;μr为每段铁芯的相对磁导率;ϕsi,k为第i个磁回路中第k段长定子内的磁通量;ϕei,k为第i个回路中第k段磁极铁芯或磁轭内的磁通量. 为在EMC模型中引入导磁材料的非线性,不再将μr简单地设置为恒定值,而是根据每段铁芯的磁通进行计算. 磁极铁芯、磁轭及长定子铁芯均采用硅钢片,牌号为M530-50A,导磁材料的非线性可通过B-H曲线体现,如图5所示.
根据文献[14],B-H曲线可采用式(10)函数进行拟合.
H=α1B+α2Bα3, (10) 式中:α1、α2及α3为拟合函数自变量B的系数,可通过对图5中B-H曲线的拟合确定.
长定子铁芯的相对磁导率可表示为
μr1=Bμ0H=1μ0(α1+α2Bα3−1). (11) 根据磁密、面积及磁通的关系,式(11)可表达为
μr1=1μ0(α1+α2(ϕsiAsi,k)α3−1). (12) 同理可求解磁极铁芯及磁轭的相对磁导率为
μr2=1μ0(α1+α2(ϕeiAei,k)α3−1). (13) 将式(12)、(13)代入式(8)、(9)求解磁极铁芯、磁轭及长定子铁芯磁阻. 通过式(5)~(9)可知,磁阻矩阵A与间隙s及磁通ϕ相关,因此,将其记为A(s,ϕ).
1.3 电路模型
悬浮电磁铁分为两个控制回路,分别由一个控制器进行供电. 控制器的输出为电压,根据控制回路的负载特性转变为相应的负载电流. 在进行电磁力模型与控制模型联合分析时,需要搭建电磁铁的电路模型,其功能是将控制模型的输入电压转变为负载电流,再结合EMC模型计算电磁力. 与EMC模型类似,仅搭建一个回路的模型,6个磁极串联实际可等效为6个电阻与6个电感的串联,如图6所示. 图中:RMj为单个磁极电阻;LMj为单个磁极电感;ULj为单个磁极电感电压;UM为单个控制回路的输入电压.
根据电路模型,单个控制回路的输入电压为
UM=RMI+6∑j=1ULj=RMI+nT∙ϕp, (14) 式中:RM为单个控制回路的总电阻.
整理式(14),控制回路电流可表达为
I=(UM−nT∙ϕp)/RM. (15) 1.4 磁力模型
式(4)给出了磁通与电流关系,式(15)给出了磁通、电流与电压关系. 将式(15)代入式(4),可得磁通与电压的关系为
A(s,ϕ)ϕ=TTn(UM−nT∙ϕp)/RM. (16) 根据磁通关系ϕp=Tϕ,式(16)整理为
TTnnTT∙ϕ = TTnUM−RMA(s,ϕ)ϕ. (17) 经过计算发现,矩阵TTnnTT为奇异矩阵,常微分式(17)很难进行求解. 因此,为便于求解方程,采用中间变量替换原变量.
根据磁通关系ϕp=Tϕ,将式(16)整理成变量为ϕp的方程,如式(18)
A(s,ϕ)T−1ϕp=TTn(UM−nT∙ϕp)/RM. (18) 进一步整理为
nTϕp=nTTA−1(s,ϕ)TTn(UM−nT∙ϕp)/RM. (19) 将6个磁极的磁通之和β作为中间变量,则β可表示为
β=6∑j=1ϕpj. (20) 将式(20)代入式(19),得到关于β的常微分方程为
nβ=nTTA−1(s,ϕ)TTn(UM−n∙β)/RM, (21) 式中:nTTA−1(s,ϕ)TTn不再是一个矩阵或向量,而是一个关于s、ϕ的变量,记为1/M (s,ϕ).
对式(21)进行整理得
˙β=UM/n−RMM(s,ϕ). (22) 依据式(15)、(22),可得I与β间的关系为
I=nM(s,ϕ)β. (23) 依据式(19)、(22)及磁通关系ϕp=Tϕ,得到ϕ与β间的关系为
ϕ=A−1(s,ϕ)TTnM(s,ϕ)nβ. (24) 通过式(22)~(24)计算出悬浮电磁铁电流以及电磁力求解所需的磁通.
根据式(5),计算各部分气隙的磁通为
ϕa,oj=ϕajRajRa,oj. (25) 基于虚功原理,各部分气隙对应的电磁力为
Fmag,oj=ϕ2a,oj2μ0Aa,oj. (26) 单个磁极电磁力为式(26)中各部分电磁力之和,即
Fmag,j=Fmag,mj+Fmag,nj+Fmag,Lj. 最后,求解半个悬浮电磁铁的电磁力为
Fmag=6∑j=1Fmag,j. 根据电磁力解析过程,EMC模型可简化为图7所示的结构框图,输入为电压及间隙,输出为电流及电磁力. 首先进行磁阻计算,并组建磁阻矩阵,而导磁材料磁阻的计算需要将磁通作为输入. 采用磁阻矩阵A进行电流及磁通计算,磁通需通过常微分方程及代数方程求解,磁通求解结果一方面用于电磁力计算,一方面反馈给导磁材料磁阻计算.
2. 模型分析及试验验证
2.1 与传统EMC模型对比
根据悬浮电磁铁及长定子的尺寸及参数(如表1所示),对本文EMC模型进行量化. 此外,将导磁材料的相对磁导率设为恒定值,搭建基于线性导磁材料的传统EMC模型. 对两个模型电磁力的计算结果进行对比分析,如图8所示.
表 1 悬浮电磁铁及长定子参数Table 1. Parameters of maglev electromagnet and long stator项点 取值 项点 取值 定子极距/mm 258.0 铁芯厚度/mm 170.0 电磁铁极距/mm 266.5 磁极匝数 300 定子齿宽度/mm 43.0 额定磁间隙/mm 12.5 定子槽宽度/mm 43.0 恒定相对磁导率 7 000 磁间隙为12.5 mm,电流在0~35 A内,两个模型的电磁力结果非常接近;当电流超过35 A时,随着电流增加,计算结果偏差增大. 原因是实际工作状态下,随着电流增大,导磁部件的磁密增大;当达到材料饱和磁密时,磁密随电流的增加率大幅降低,电磁力也相应地出现饱和现象,而传统EMC模型并未考虑材料的磁饱和. 因此,传统EMC模型适用于小电流区间,一般应用在工作点附近的线性区间20~30 A. 而大电流区间与实际工作情况不符,例如在故障、起浮、降落等特殊工况时,模型精度大幅降低,无法用于电磁力计算及系统特性分析.
2.2 与有限元模型对比
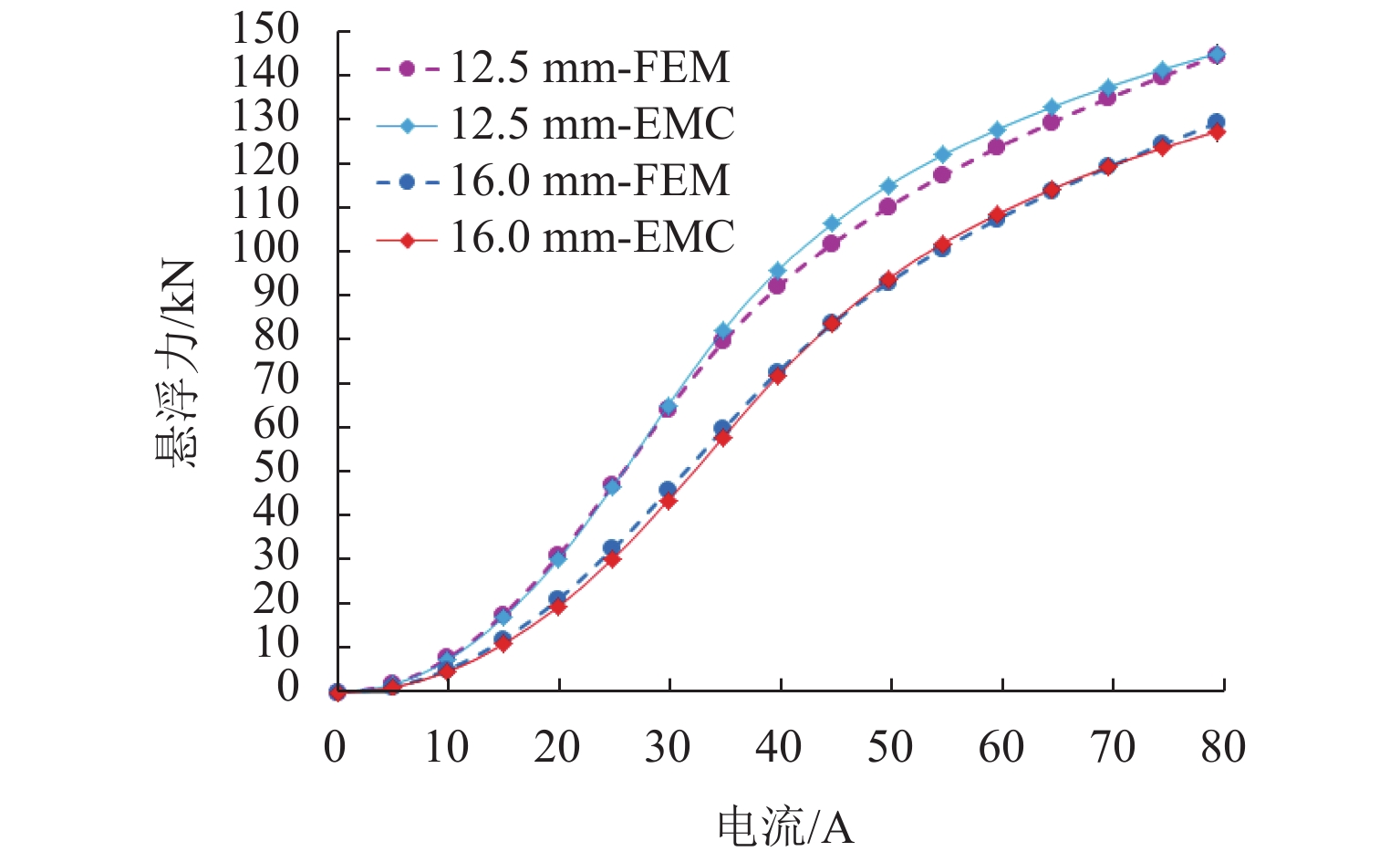
为验证本文提出的EMC模型准确性,搭建了悬浮电磁铁与长定子FEM模型,如图9所示,两者电磁力的计算结果如图10所示. 磁间隙12.5 mm与16.0 mm,电流0~80 A内,两者电磁力的计算结果具备非常高的一致性,均存在饱和现象;磁间隙12.5 mm,电流50 A时,电磁力偏差最大,EMC计算结果为115 kN,FEM计算结果为110 kN,偏差仅为4.5%,这表明了基于非线性材料的EMC模型具有较高的准确性.
2.3 试验验证
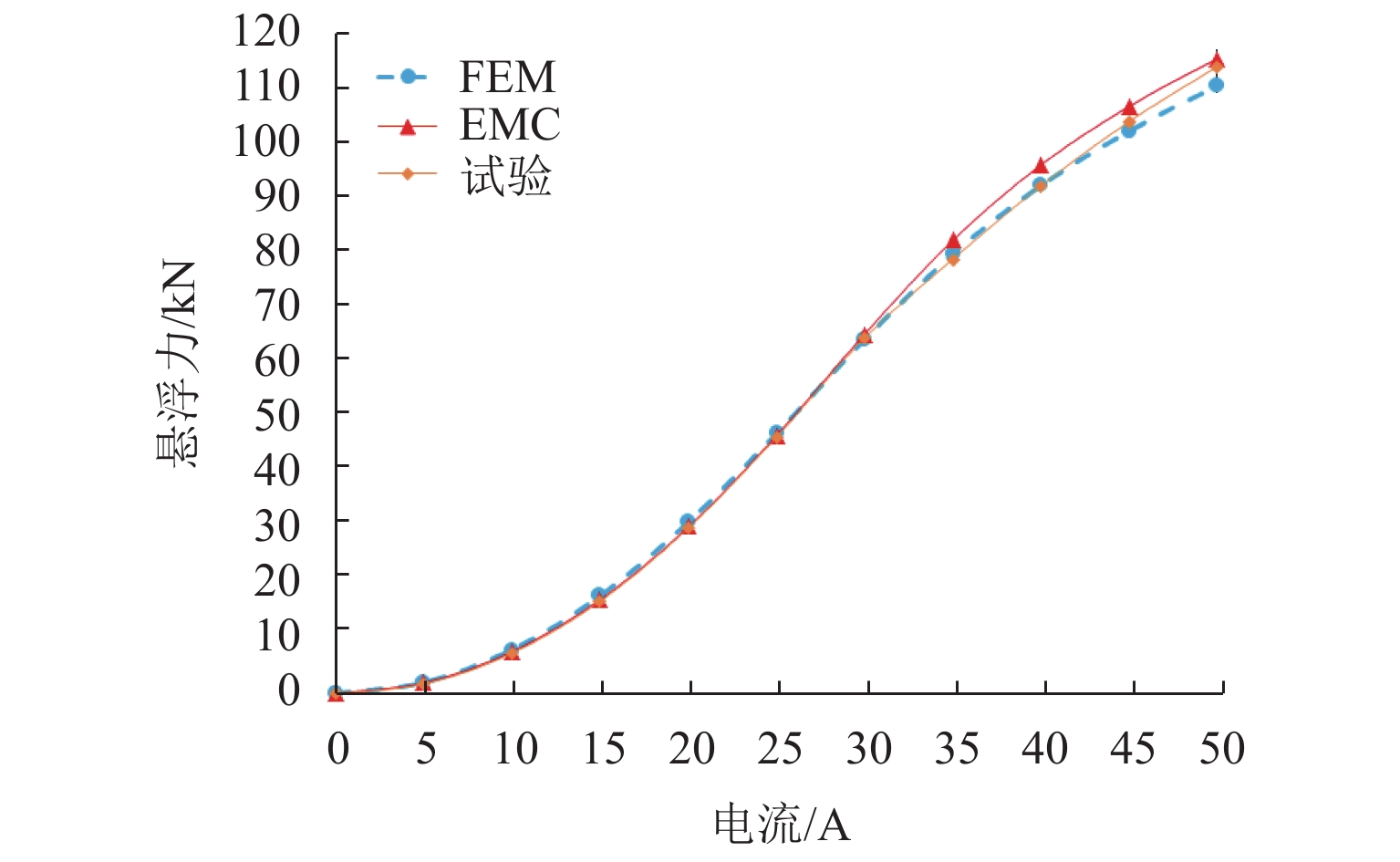
针对高速磁浮电磁铁特性研究,搭建了地面试验平台,对悬浮电磁铁的静态电磁力进行测试,如图11所示. 试验台通过液压系统调整长定子与悬浮电磁铁的间隙;采用两路电源供电,但受最大输出电流限制,仅对0~50 A电流进行测试,步长为5 A;通过力传感器检测电磁铁与长定子间的电磁力. 磁间隙12.5 mm下电磁力的测试结果与EMC及FEM的计算结果对比如图12所示.
额定工况下,悬浮电磁铁的工作点:磁间隙为12.5 mm,电流为25 A,电磁力约为46 kN. 在工作点处,EMC、FEM及试验测试的电磁力结果几乎相同,在其他电流值下,电磁力结果偏差也极小,从而进一步验证了本文EMC模型以及所搭建FEM模型的准确性.
3. 结 论
本文基于非线性材料搭建了高速磁浮悬浮电磁铁的磁路、电路及磁力模型,将计算结果与传统EMC模型进行对比分析,并通过有限元及试验验证,通过对模型研究分析,得到以下结论:
1) 搭建悬浮电磁铁EMC模型时,采用了非线性导磁材料,通过引入B-H曲线的拟合函数,将导磁材料的非线性及饱和特性体现在模型中.
2) 无论小电流区,还是大电流区,本文EMC模型求解的电磁力均与实际情况接近,相比传统EMC模型,结果更加准确,适用范围更广.
3) 本文EMC模型能够快速、准确地求解电磁力,且通过电路模型实现与控制模型的良好匹配,因此,可通过联合仿真对悬浮系统动态特性进行深入分析,为悬浮系统设计及参数优化提供了依据.
-
表 1 轴承故障样本
Table 1. Bearing failure samples
轴承状态 故障点直径/mm 训练集 测试集 正常 — 60 60 内圈故障 0.178 60 60 滚动体故障 0.178 60 60 外圈故障 0.178 60 60 内圈故障 0.356 60 60 滚动体故障 0.356 60 60 外圈故障 0.356 60 60 内圈故障 0.533 60 60 滚动体故障 0.533 60 60 外圈故障 0.533 60 60 表 2 3种分类结果
Table 2. Classification results for the three methods
模型 迭代时间/s 正确率/% EEMD_H模型 282.9 99.43 EEMD模型 149.8 94.17 EMD_H模型 304.3 95.10 表 3 FWA、PSO、GA对SVM参数寻优
Table 3. FWA,PSO,and GA for SVM parameter optimisation
算法 C σ 正确率/% PSO 38.12 9.35 98.67 FWA 35.39 6.88 99.00 GA 57.86 23.97 98.67 表 4 3种分类结果
Table 4. Classification results for the three algorithms
模型 迭代时间/s 正确率/% FWA 14.4 99.63 GA 114.3 99.20 PSO 282.9 99.43 -
TANDON N, CHOUDHURY A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings[J]. Tribology International, 1999, 32(8): 469-480. 于德介, 程军圣, 杨宇. 机械故障诊断的Hilbert-Huang变换方法[M]. 北京: 科学出版社, 2006: 4-12 HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sciences, 1998, 454: 903-995. 黄建,胡晓光,巩玉楠. 基于经验模态分解的高压短路机械故障诊断方法[J]. 中国电机工程学报,2011,31(12): 108-113.HUANG Jian, HU Xiaoguang, GONG Yumin. Model fault diagnosis method of high voltage short circuit based on empirical mode decomposition[J]. Proceeding of the CSEE, 2011, 31(12): 108-113. 时培明,李庚,韩冬颖. 基于改进 EMD的旋转机械耦合故障诊断方法研究[J]. 中国机械工程,2013,24(17): 2367-2372.SHI Peiming, LI Geng, HAN Dongying. Study on coupling fault diagnosis method of rotating machinery based on improved EMD[J]. China Mechanical Engineering, 2013, 24(17): 2367-2372. WU Z, HUANG N. Ensemble empirical mode decomposition:a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. 秦娜,金炜东,黄进,等. 基于EEMD样本熵的高速列车转向架故障特征提取[J]. 西南交通大学学报,2014,49(1): 27-32.QIN Na, JIN Weidong, HUANG Jin, et al. Fault feature extraction of high-speed train bogies based on eemd sample entropy[J]. Journal of Southwest Jiaotong University, 2014, 49(1): 27-32. AlVAR M, SANCHEZ A, ARRANZ A. Fast background subtraction using static and dynamic gates[J]. Artificial Intelligence Review, 2014, 41(1): 113-128. 何青,褚东亮,毛新华,等. 基于EEMD和 MFFOA-SVM滚动轴承故障诊断[J]. 中国机械工程,2016,27(9): 1191-1197.HE Qing, ZHU Dongliang, MAO Xinhua, et al. Fault diagnosis of rolling bearing based on EEMD and MFFOA-SVM[J]. China Mechanical Engineering, 2016, 27(9): 1191-1197. TAN Y, ZHU Y. Fireworks algorithm for optimization [C]//International Conference in Swarm Intelligence. Berlin: Springer, 2010: 355-364 顾军华,赵燕,董瑶. 基于FWA-SVM的室内无线定位研究[J]. 河北工业大学学报,2016,45(6): 35-40.GU Junhua, ZHAO Yan, DONG Yao. Study on indoor wireless location based on FWA-SVM[J]. Journal of Hebei University of Technology, 2016, 45(6): 35-40. 高宏宾,侯杰,李瑞光. 基于核主成分分析的数据流降维研究[J]. 计算机工程与应用,2013,49(11): 105-109.GAO Hongbin, HOU Jie, LI Ruiguang. Research on dimension reduction of data flow based on kernel principal component analysis[J]. Computer Engineering and Applications, 2013, 49(11): 105-109. 陈维荣,关佩,邹月娴. 基于SVM的交通事件检测技术[J]. 西南交通大学学报,2011,46(1): 63-67.CHEN Weirong, GUAN Pei, ZOU Yuexian. A traffic event detection technology based on SVM[J]. Journal of Southwest Jiaotong University, 2011, 46(1): 63-67. 于世飞,齐丙娟,谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报,2011,40(1): 2-10.YU Shifei, QI Bingjuan, TAN Hongyan. Study on support vector machine theory and algorithm[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(1): 2-10. 叶林,刘鹏. 基于经验模态分解和支持向量机的短期风电功率组合预测模型[J]. 中国电机工程学报,2011,31(31): 102-108.YE Lin, LIU Peng. Study on short-term wind power combination forecasting model based on empirical mode decomposition and support vector machine[J]. Proceeding of the CSEE, 2011, 31(31): 102-108. 谭营,郑少秋. 烟花算法研究进展[J]. 智能系统学报,2014(5): 515-528.TAN Ying, ZHENG Shaoqiu. Research progress of fireworks algorithm[J]. Journal of Intelligent Systems, 2014(5): 515-528. 张乾, 基于振动信号的轴承状态监测和故障诊断方法研究[D]. 长沙: 中南大学, 2012 张敏,程文明,刘娟. 复杂生产过程小故障诊断与分类方法研究[J]. 西南交通大学学报,2014,49(5): 842-847.ZHANG Min, CHENG Wenming, LIU Juan. Study on fault diagnosis and classification of complex production processes[J]. Journal of Southwest Jiaotong University, 2014, 49(5): 842-847. -






 下载:
下载:











 下载:
下载: