面向遥感影像匹配的特征点检测算子性能评估

叶沅鑫; 慎利

doi:10.3969/j.issn.0258-2724.2016.06.017

面向遥感影像匹配的特征点检测算子性能评估

doi: 10.3969/j.issn.0258-2724.2016.06.017

叶沅鑫^1,2,
慎利^1, ,

基金项目:

国家973计划资助项目（2012CB719901）

国家自然科学基金资助项目（41401369，41401374）

详细信息

作者简介:
叶沅鑫(1985-),男,讲师,研究方向为遥感图像处理,E-mail:yeyuanxin110@163.com

通讯作者:
慎利(1986-),男,讲师,研究方向为机器学习与遥感影像处理,E-mail:rsshenli@outlook.com

计量
- 文章访问数: 578
- HTML全文浏览量: 92
- PDF下载量: 267
- 被引次数: 0
出版历程
- 收稿日期: 2015-09-16
- 刊出日期: 2016-12-25

Performance Evaluation of Interest Point Detectors for Remote Sensing Image Matching

YE Yuanxin^1,2,
SHEN Li^{1
, ,}

摘要

摘要: 在基于特征点的匹配方法中，特征点检测是非常关键的步骤，直接影响到匹配的效果.为了确立遥感影像匹配过程中特征点算子的选择依据，本文从光谱、时相和尺度（分辨率）3个方面，选择不同类型的遥感影像作为实验数据，以特征点重复率作为评估标准，对当前主流的Harris-Laplace、Hessian-Laplace、DoG和MSER 4种特征点检测算子进行性能评估，并分析了每一种算子的优缺点和适用范围.实验结果表明：在光谱和时相方面，Hessian-Laplace的平均重复率达到40%，性能最好，其次为Harris-Laplace和DoG，而MSER的性能相对较弱；而对于尺度方面，MSER表现出最好的性能，平均重复率达到35%，其次为Hessian-Laplace，而Harris-Laplace和DoG的性能较弱.
- 遥感影像 /
- 影像匹配 /
- 特征点检测 /
- 重复率
Abstract: Interest point detection is a crucial step for the image matching because it directly influences the matching results. In order to establish the criterion of selecting the interest point detectors for remote sensing image matching, different remote sensing images in terms of spetrum, time and scale were selected to evaluate the four famous interest point detectors including Harris-Laplace, Hessian-Laplace, Difference of Gaussian (DoG) and Maximally Stable Extremal Regions (MSER), and the repeatability was used as the evaluation criterion. The merits, the demerits and application of these detectors were also discussed. The experimental results show that for spectrum and time variation, the repeatability of Hessian-Laplace detector achieves 40% whichperforms best, followed by Harris-Laplace and DoG, whereas MSER performs worst. For image scale changes, MSER outperforms other detectors and its repeatability is 35%, followed by Hession-Laplace, whereas Harris-Laplace and DoG perform worse than other detectors.
- remote sensing images /
- image matching /
- interest point detection /
- repeatability

HTML全文

随着我国西部山区大跨桥梁蓬勃发展^[1-2]，复杂山区桥梁桥址区风场环境模拟日益受到重视^[3-4]. 而山区地形高低起伏，高度差异较大^[5]，在地形风场试验中不可避免会截断地形，截断地形的高度突变对来流特性将产生明显影响^[6-8]. 此时，在地形模型边界添加过渡段统一高低不平的地形边线是一种有效方法，所以，研究地形边界过渡段对复杂地形区桥梁风场研究具有重要意义^[9-11].

目前，国内外学者对地形模型边界过渡段已有一定研究：胡朋等^[12]推导出一类基于势流理论下圆柱绕流流线的地形模型过渡段曲线线型，并和斜坡过渡段对比，验证了其作为过渡段的适用性和优越性；靖洪淼等^[13]对基于双曲正切函数的过渡段流动特性进行了研究；Uchida等^[14]基于大涡模拟的方法对复杂地形上风场减速效应和流动分离进行了模拟研究.

然而，目前过渡段的设置原则及其合理形式仍未达成统一认识，绕兰金物体不可压缩无旋流动流场线及平方正弦曲线作为过渡段线型的可行性有待明确. 本文通过数值模拟的方式对比了上述2类线型与目前常用的双曲正切函数及平板风场线型的流动特性，并提出了地形模型边界过渡段线型构造的新原则，可以为地形桥址区的CFD （计算流体力学）模拟提供一定参考价值.

1. 过渡段设置原则

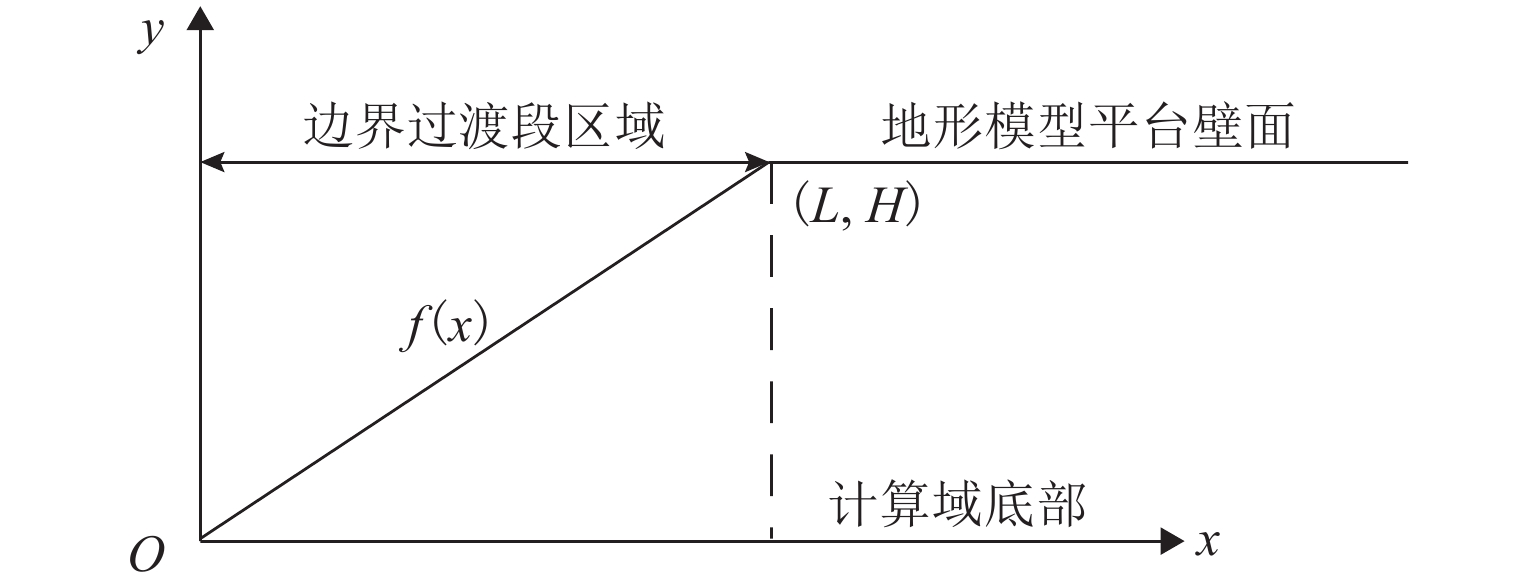
在桥址区风特性研究中，需先截取桥位处附近的一部分地形，后将其生成为几何固定壁面供后续的风洞试验或数值模拟使用. 截取地形常存在较大的起伏，致使地形模型与风洞地面或计算域底面存在高差，造成了不真实的台阶，如图1所示. 图中：x为水平方向位置，y为高程（L，H）为地形与过渡段曲线f(x)与地形平台的接触点坐标. 地形模型边缘台阶的存在使来流接触台阶，而后产生流动分离、局部空化现象和湍流转捩等与实际风场不符的现象，导致流场和实际来流产生明显不同. 该现象对地形范围较小、地形起伏大的桥址区风场结果影响尤其显著. 为此，设置过渡段来衔接不同高度的模型边界和风洞地板或数值模拟计算域底面，以实现来流从入口到地形区域的风场贴近实际情况.

图 1 地形模型边界

Figure 1. Terrain model boundary

下载: 全尺寸图片幻灯片

在桥址区地形风洞试验中常以风洞初始风场为参照，因此，试验中要求风洞来流由地面过渡到截取地形边缘时，其风场应尽量与参考风场保持相同的特性^[12-13]，避免发生来流与壁面分离.

存在逆压梯度和黏性力是来流接触地形边缘台阶后产生分离的原因. 以斜坡线型为例，流体动量方程如式（1）.

$\begin{array}{c} \dfrac{{\rm{d}}{U}_{\rm{i}}}{{\rm{d}}t}={f}_{\mathrm{i}}-\dfrac{1}{\rho }\dfrac{\partial p}{\partial {x}_{\mathrm{i}}} + \dfrac{\mu }{\rho }\dfrac{\partial }{\partial {y}_{{\rm{i}}}}\left(\dfrac{\partial {U}_{\mathrm{i}}}{\partial {y}_{{\rm{i}}}}\right)\text{，}\end{array}$

(1)

式中：U_i为流体速度，f_i为流体所受体积力，p为当前位置压强，ρ为流体密度，μ为黏性力系数，$ x_{\rm{i}} $、$ y_{\rm{i}} $为$ x $、$ y $方向的2个位移分量，t为时间.

速度的突然变化将造成压力的突然变化，由此可以得出2种过渡段构造思路：

1）为使来流速度流经过渡段时平稳连续，可认为流线的过渡段线型应保持一阶导数连续. 类似地，考虑到黏性力的影响，流体加速度也应避免突变，过渡段线型应保持二阶导数连续. 由此，过渡段曲线f(x)需满足二阶导数连续和式（2）边界条件.

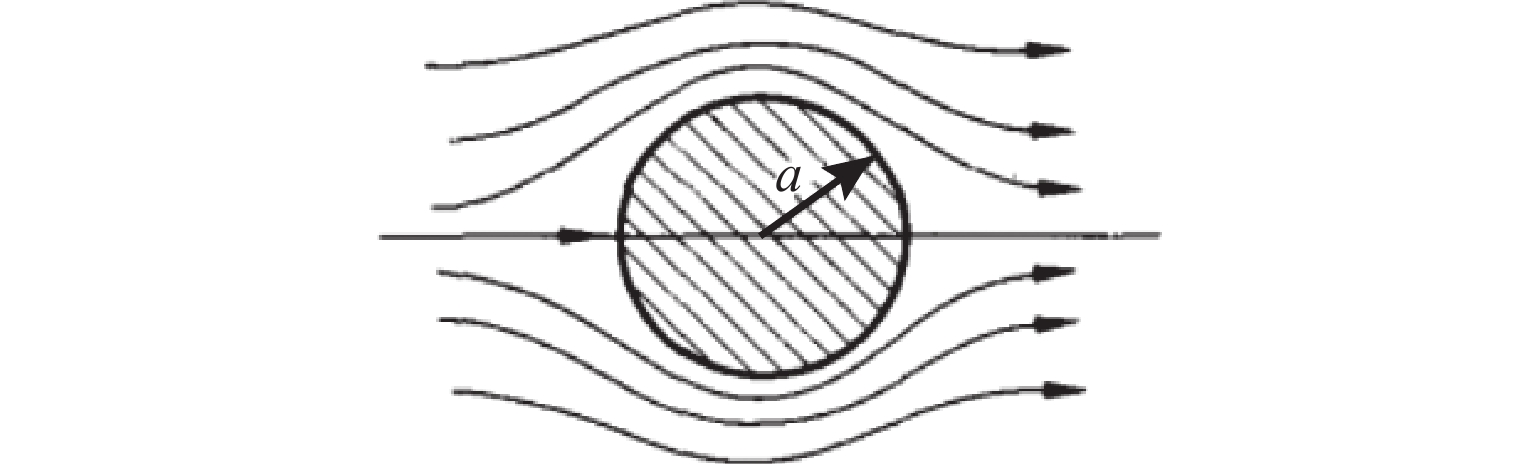
$\begin{array}{c}\left\{\begin{array}{c}f\left(0\right)=0,\;f\left(L\right)=H,\\ \dot{f}\left(0\right)=0,\;\dot{f}\left(L\right)=0,\\ \ddot{f}\left(0\right)=0,\;\ddot{f}\left(L\right)=0. \end{array}\right.\end{array}$

(2)

2）在势流场假定中各流线上的点满足流动不分离，各流线可视为彼此独立互不影响的气流，可认为气流在各流线上经过时性质不受影响，因此，可将流线线型作为过渡段线型. 图2所示为圆柱绕流流线. 图中：a为圆球半径. 通常选取已有解析表达式的流线，先考虑过渡段的边界条件，再进行截取，构造过渡段曲线.

图 2 理想流体圆柱绕流流线

Figure 2. Streamlines around an ideal fluid cylinder

下载: 全尺寸图片幻灯片

由上述2种构造过渡段思路出发，提出构造过渡段线型的2个原则：

1）过渡后的气流特性（如风速、风攻角和湍流强度等）应尽量与未受扰动的参考风场特性保持一致. 不能出现流动分离，因为气流分离会使边界层增厚、出现气流不稳定等现象.

2）气流从过渡段开始到达到稳定时的过渡总长度应尽可能短，较长的气流过渡总长度会进一步减小地形模型的有效区域，对于数值模拟方法，也会相应地增大计算区域尺寸、增加计算工作量.

2. 过渡段线型选取

目前，在地形模型风洞试验和CFD模拟中，主要的过渡段线型有：斜坡、理想流体圆柱绕流场流线、维多辛斯基曲线和双曲正切函数. 相较于其他主要过渡段线型，平方正弦曲线斜率变化均匀、一阶和二阶连续可导，对来流风场影响较小，符合上文提出的过渡段线型构造原则，是比较理想的过渡段线型. 为探究不同流线形式作为过渡段线型的适用性，本节利用平方正弦曲线分别使用第1节的思路1、2绘制典型过渡段线型并进行对比，研究其在作为过渡段时展现的气动特性. 结合上文提出的2个原则综合判断上述流线及其对应解析函数在地形模型过渡段问题上的适用性，本节选用双曲正切函数作为思路1的典型过渡段线型. 常见的具有解析式的流线线型：绕金兰物体的不可压缩无旋流动、均匀来流绕圆球流动等，选用绕兰金物体的不可压缩无旋流动函数作为思路2的过渡段线型.

2.1 平方正弦函数及双曲正切函数的过渡段曲线

用于过渡段曲线的平方正弦函数、双曲正切函数分别如式（3）、（4）.

$f_1\left(x\right)={h\mathrm{s}\mathrm{i}\mathrm{n}}^{2}\dfrac{{\text{π}} x}{2l}\text{，}$

(3)

$f_2\left(x\right)=\dfrac{h}{2}\left[\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(\dfrac{2cx}{l}-c\right) + 1\right]\text{，}$

(4)

式中：h为台阶高度差；l为过渡段长度；c为在tanh x中截取的单边长度，本节取4（一般取$ c\geqslant 3 $）.

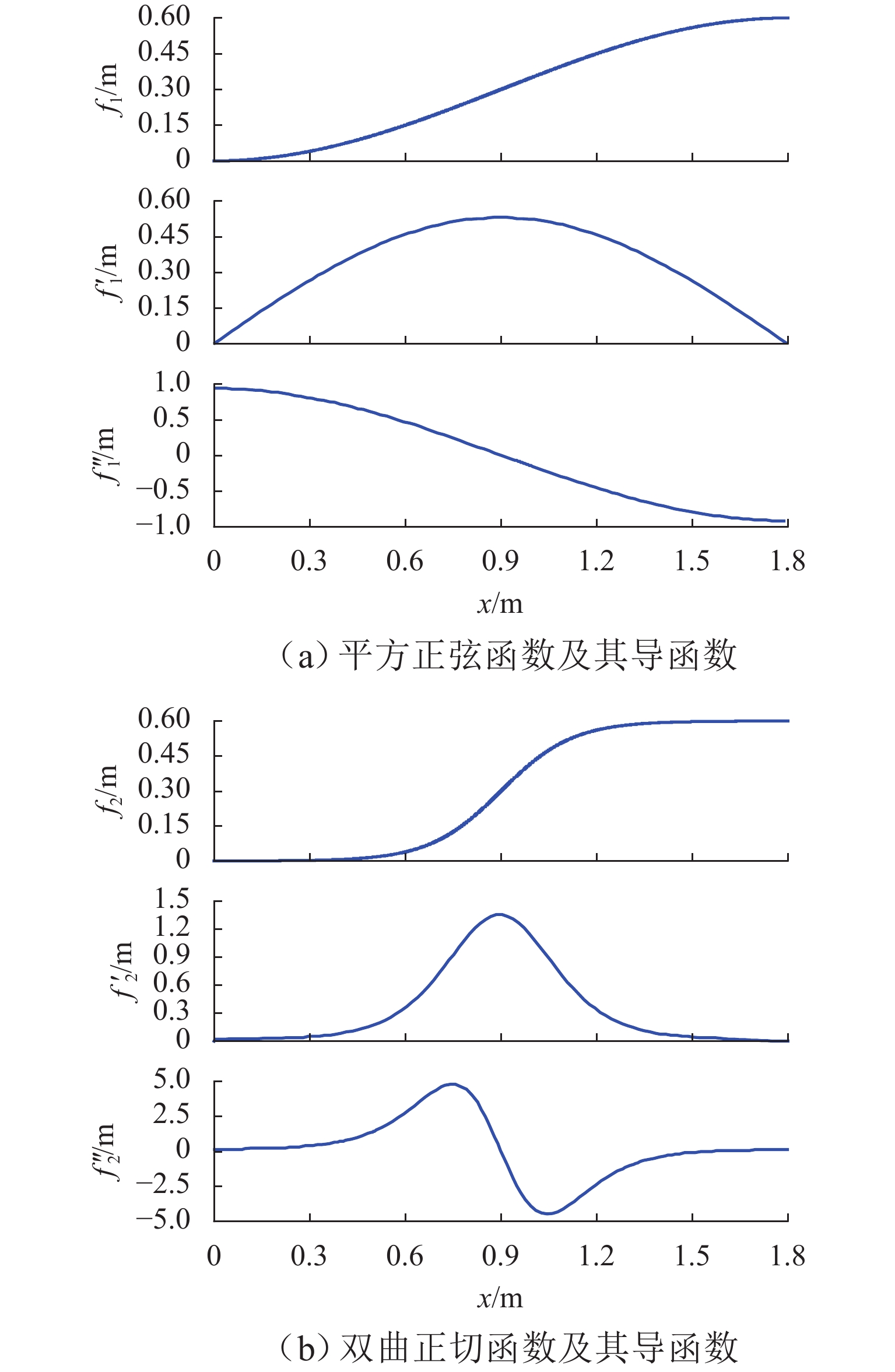
平方正弦函数、双曲正切函数及其一、二阶导数如图3所示. 由图可见，平方正弦函数及其一阶导数在边界处连续，满足式（2）边界条件的前2项；双曲正切函数满足式（2）中的全部条件.

图 3 用于过渡段的2种函数及其导函数

Figure 3. Two functions and their derivatives used for transition segments

下载: 全尺寸图片幻灯片

2.2 绕兰金物体过渡段曲线

绕兰金物体不可压缩无旋流动流函数为

$\begin{split} &\varPsi =-\frac{1}{2}{U}_{\mathrm{\infty }}{y}^{2} + \frac{1}{4{\text{π}} }\frac{Q\left(x + d\right)}{\sqrt{{\left(x + d\right)}^{2} + {y}^{2}}}-\\ &\quad \frac{1}{4{\text{π}} }\frac{Q\left(x-d\right)}{\sqrt{{\left(x-d\right)}^{2} + {y}^{2}}}, \end{split}$

(5)

式中：$ {U}_{\infty } $为给定的来流速度，Q为源强，d为点源到点汇距离的一半.

令$ {b}^{2}=\dfrac{Q}{2{\text{π}} {U}_{\infty }} $，则有

$-\frac{2\varPsi }{{U}_{\mathrm{\infty }}}={y}^{2}-\frac{{b}^{2}\left(x + d\right)}{\sqrt{{\left(x + d\right)}^{2} + {y}^{2}}} + \frac{{b}^{2}\left(x-d\right)}{\sqrt{{\left(x-d\right)}^{2} + {y}^{2}}}.$

(6)

对流函数求导，可得其与速度场之间的关系为

$\begin{split} &{v}_{x}=\frac{1}{y}\frac{\partial {\varPsi }}{\partial y}=-\frac{{U}_{\mathrm{\infty }}}{2y}\times\\ &\quad \left(2y + \frac{{b}^{2}y\left(d-x\right)}{{\left({y}^{2} + {\left(d-x\right)}^{2}\right)}^{\tfrac{3}{2}}} + \frac{{b}^{2}y\left(d + x\right)}{{\left({\left(d + x\right)}^{2} + {y}^{2}\right)}^{\tfrac{3}{2}}}\right)\text{，} \end{split}$

(7)

$\begin{split} &{v}_{y}=-\frac{1}{x}\frac{\partial \varPsi }{\partial x}=\left(\frac{{b}^{2}}{\sqrt{{y}^{2} + {\left(d-x\right)}^{2}}}-\frac{{b}^{2}}{\sqrt{{y}^{2} + {\left(d + x\right)}^{2}}}-\right.\\ &\quad \left.\frac{{b}^{2}\left(d-x\right)\left(2b-2x\right)}{2{\left({y}^{2} + {\left(d-x\right)}^{2}\right)}^{\tfrac{3}{2}}} + \frac{{b}^{2}\left(d + x\right)\left(2b + 2x\right)}{2{\left({y}^{2} + {\left(d + x\right)}^{2}\right)}^{\tfrac{3}{2}}} \right) \frac{{U}_{\mathrm{\infty }}}{2y}, \end{split}$

(8)

式中：v_x、v_y分别为横向速度场和垂直速度场.

兰金物体半长轴长度R、半短轴长度S与b、d的关系为

$\left\{\begin{array}{l} \left({R}^{2}-{d}^{2}\right)=2{b}^{2}Rd,\\ {S}^{2}=\dfrac{2{b}^{2}d}{\sqrt{{S}^{2} + {d}^{2}}}. \end{array}\right.$

(9)

式（6）引入参数m可得流线方程通式为

$\begin{split} & E\left(x,y\right)={y}^{2}-\frac{{b}^{2}\left(x + d\right)}{\sqrt{{\left(x + d\right)}^{2} + {y}^{2}}} +\\ &\quad \frac{{b}^{2}\left(x-d\right)}{\sqrt{{\left(x-d\right)}^{2} + {y}^{2}}}-m=0. \end{split}$

(10)

由于过渡段曲线在其起点和终点处斜率为0，可得$ {x}_{1}=\pm \mathrm{\infty } $，$ {x}_{2}=0 $，起点不可能取到无穷远处，故取斜率较小的点作为起点. 当$ x=\pm \mathrm{\infty } $时，式（10）变为$ {y}^{2}-m=0 $，可推得$ y=\pm \sqrt{m} $为流场线的渐近线.

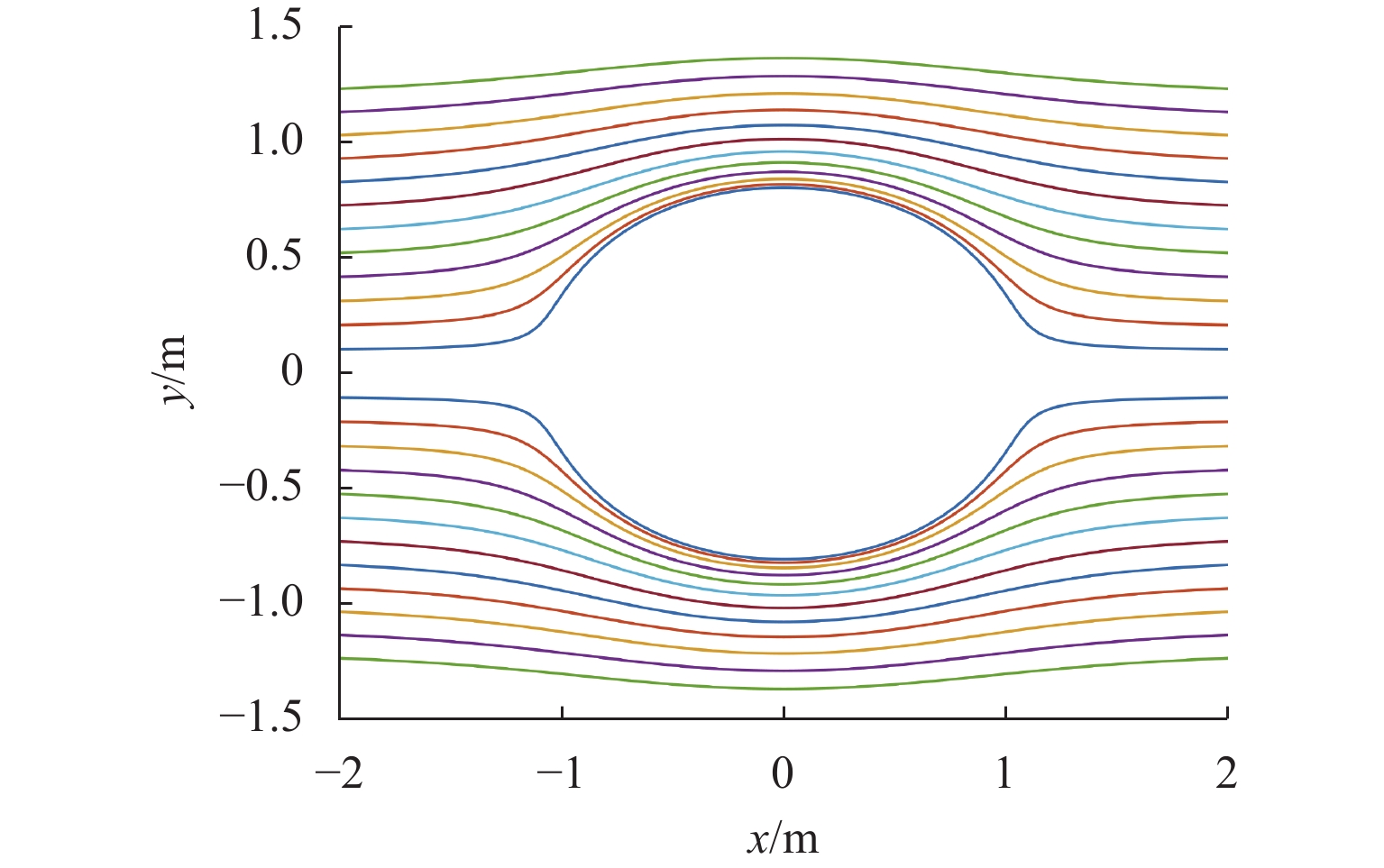
在构造过渡段曲线时，通常已知来流边界和地形模型之间的高差即台阶高度差h和过渡段等效斜率l. 因此，不妨建立绕流兰金体的S、R和h、l之间的经验关系式，经式（9），求得b和d的值，再结合过渡段曲线应满足的边界条件确定出可作为过渡段的流线方程. 本节中取h=0.6 m，l=1/3，S=4/(3H)=0.8 m，R=h/(2l) + h/10=0.96 m，由式（9）联立方程组，解得b=0.745，d=0.565，将b、d代入式（10），绘制流场线，如图4所示.

图 4 绕兰金物体不可压缩无旋流动流场线

Figure 4. Streamline of incompressible irrotational flow around Rankin body

下载: 全尺寸图片幻灯片

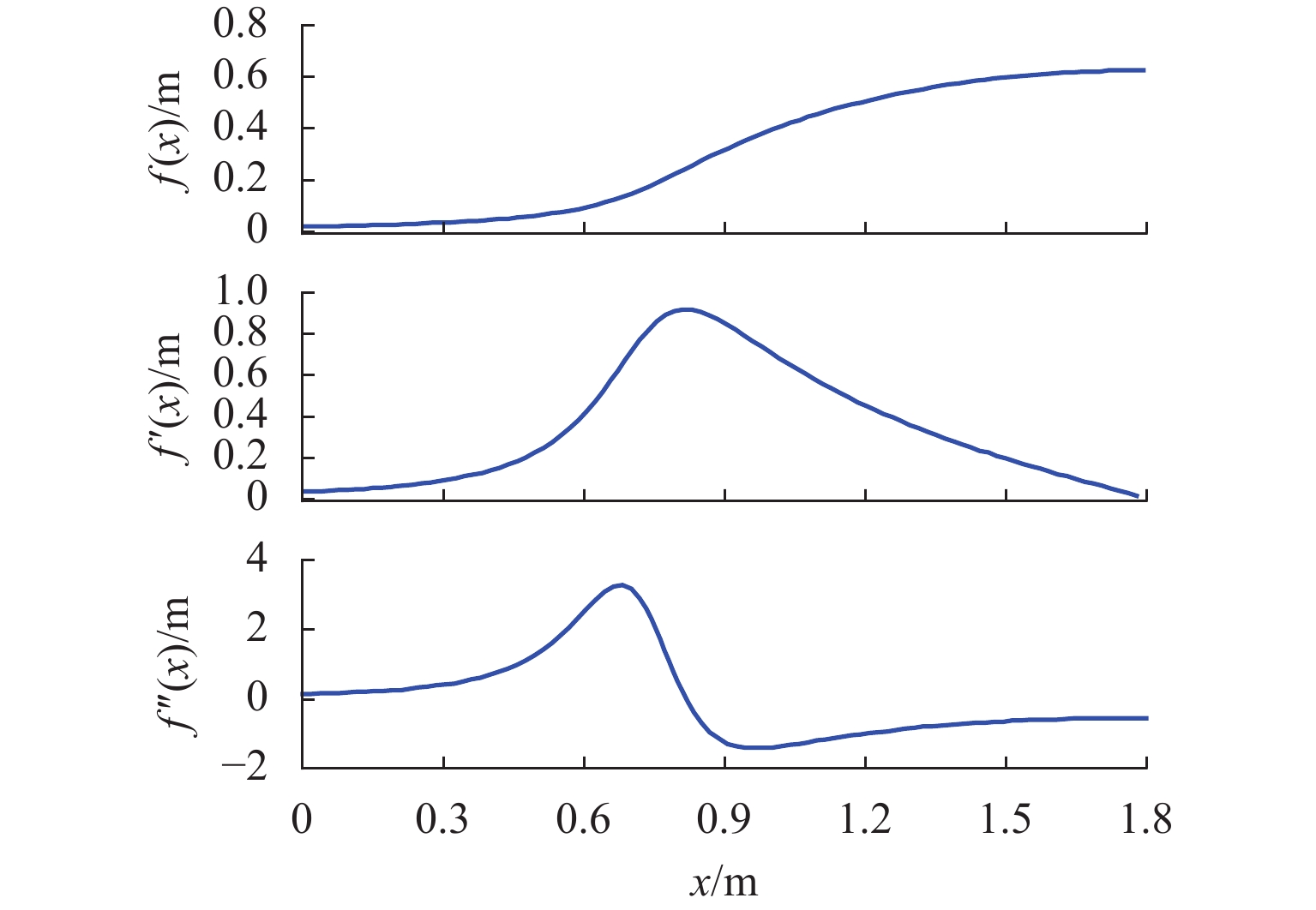
求解方程$ y\left(0\right)-y\left(-\infty \right)=h $，可得m=0.04，绘制该流场线及其一阶、二阶导数线型如图5所示. 其中，流场线可作为地形边界过渡段曲线使用.

图 5 用于过渡段的流场线及其导函数

Figure 5. Flow field lines and derivatives for transition section

下载: 全尺寸图片幻灯片

由图5可见：虽然该线型是基于第1节中第2种思路为指导绘出，但在$ \left|x\right|\geqslant 2 $时，该线型也满足第1种思路中的二阶连续可导. 因此，将式（10）作为地形边界过渡段曲线是比较合理的.

3. 数值模型及工况设置

本研究采用CFD数值模拟的方法对比分析气流经过平方正弦函数、绕兰金物体不可压缩无旋流动流线、双曲正切函数流线过渡段前后的流场分布、变化过程，计算工况如表1所示.

表 1 计算工况

Table 1. Working conditions for calculation

计算工况	A	B	C	D
过渡段形式	平板参考风场	兰金物体绕流流线	双曲正切函数	平方正弦函数

下载: 导出CSV

| 显示表格

为加快运算速度，设置二维理想台阶模型为地形，以未设置台阶处平板风场为参考风场. 取h=0.6 m，平台长度为9 m，过渡段等效斜率l=1/3，过渡段长度为1.8 m，计算域长度为50 m，高度为18 m，阻塞率设为3.3%以满足规范的要求（小于5%）.

流体经过渡段流经区域，选用结构化四边形网格进行离散. 为准确计算黏性子层的流动，要求壁面首层网格$ {y}^ + \leqslant 1 $. 基于光滑平板湍流边界层理论，估算边界层第1层网格高度为4 × 10⁻⁴ m，边界层内网格高度增长因子取为1.05，边界层以上网格高度增长因子取为1.10. 网格水平方向大小在过渡段处适当加密，各工况计算模型的网格数量见表2.

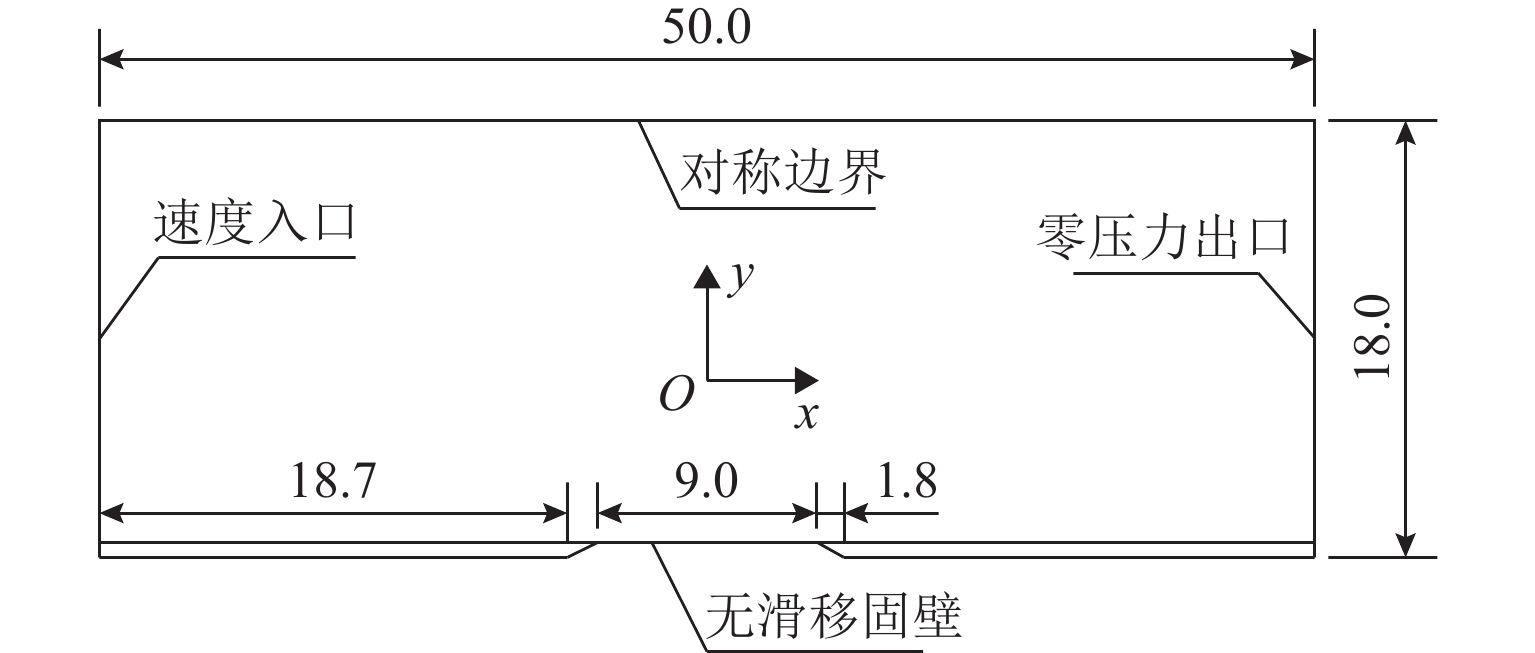
表 2 网格数量

Table 2. Number of grids 万个

计算工况	A	B	C	D
网格数	244.000	390.230	100.750	281.212

下载: 导出CSV

| 显示表格

设置模型计算域的上边界为对称边界，设置底边为无滑移固定壁面，左边界设置为速度入口，计算域右边界面设置为零压力出口，来流设置为1 m/s的均匀流，方向垂直于入口边界，湍流强度根据一般情况下风洞试验均匀流要求设置为0.5%. 计算区域及边界条件设置如图6所示.

图 6 计算区域及边界条件（单位：m）

Figure 6. Calculation area and boundary conditions (unit: m)

下载: 全尺寸图片幻灯片

数值模拟使用FLUENT软件，为获得更好的近壁面流动解析度，湍流模型使用SST k-ω模型（k为湍流动能密度，ω 为湍流比耗散率），流体设置为不可压缩定常流计算. 采用压力基耦合求解器进行计算，动量方程、湍动能方程及湍流耗散率方程均采用二阶离散格式. 计算收敛精度设置为$ 1\times {10}^{-6} $. 首层网格$y^+ $值如表3所示. 可见：对工况A、B、D，满足采用SST k-ω模型精确计算黏性底层流动时对$y^+ $值的要求（<1.0）；对工况C， $y^+ $值大于1.0的壁面范围较小，仅出现在局部个别单元；所有模型的$y^+ $均值均小于0.6，网格划分情况符合计算要求.

表 3 不同工况首层网格$y^+ $值

Table 3. $y^+ $ values of the first layer grid under different working conditions

计算工况	$y^+ $最大值	$y^+ $平均值
A	0.7615	0.5674
B	0.9946	0.5334
C	1.3259	0.5251
D	0.9808	0.5338

下载: 导出CSV

| 显示表格

为分析流体流经过渡段后不同工况下的风剖面、风攻角等沿程变化情况，即不同过渡段线型的过渡效果，在高度为0.602～1.100的高度区间内选取了26个监控点：在y=0.602～0.610以0.002为间距设置5个监控点；在y=0.610～0.650以0.005为间距设置8个监控点；在y=0.650～1.100以0.010为间距设置13个监控点. 每组监控点沿壁面法向在x=−4.5，−4.0，−3.5，−2.5，−1.5，0处分别设置了6组监控点，分别设置在过渡段的终点到模型中点之间.

4. 不同过渡段曲线流动特性分析

4.1 不同线型过渡段的气流分离特性

是否能够有效抑制来流产生流动分离是衡量地形边界过渡段线型是否适用的重要标准，因为来流流动分离后将可能产生诸如转捩成湍流和局部空化等现象，从而对风场模拟的精度和计算效率产生很大影响.

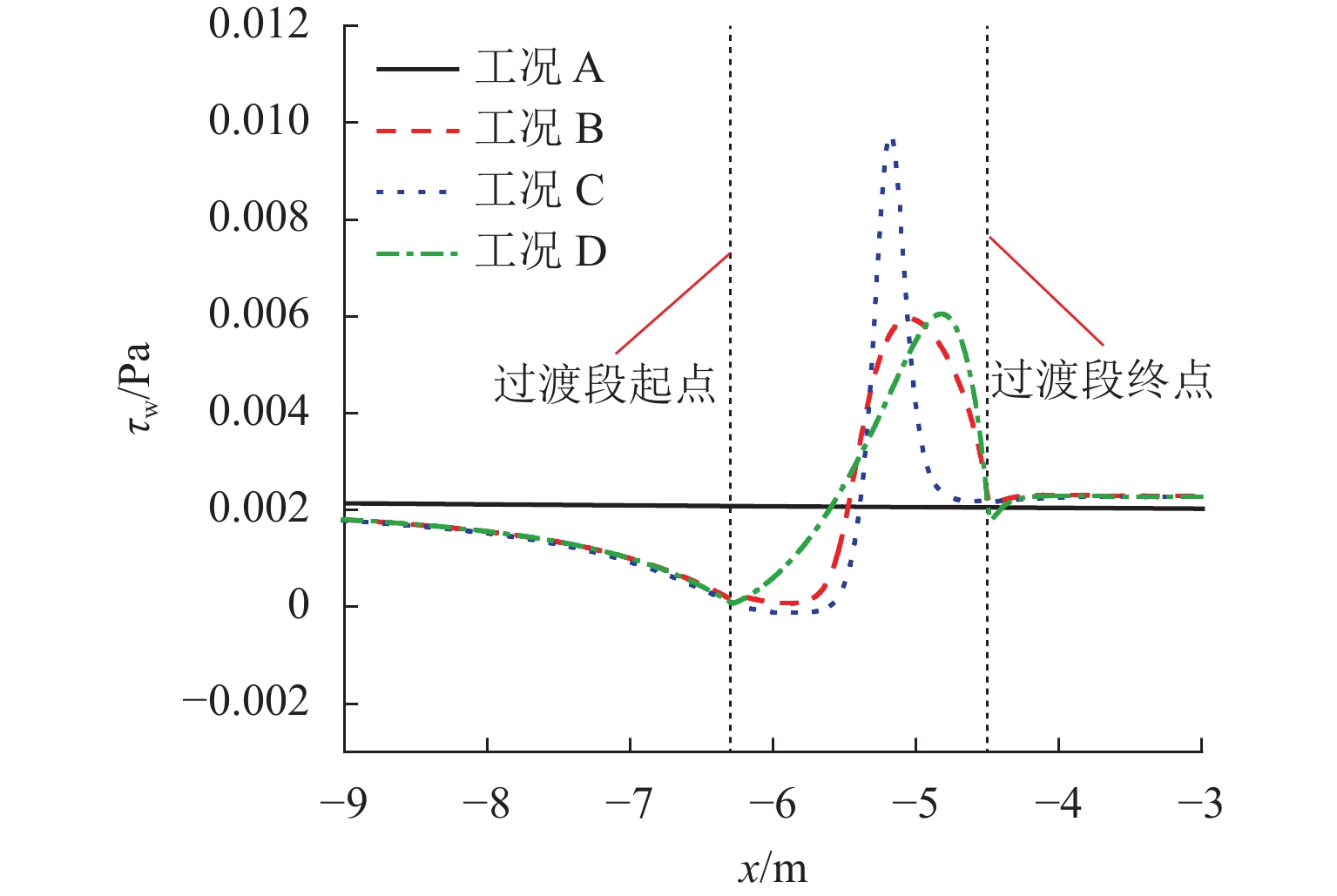
流体流经几何壁面时存在足够大的逆压梯度是产生来流流动分离的主要原因，此时流体流速将沿流向逐渐降低且有可能降低至负数（式（1）），从而出现回流现象，导致来流产生分离. 据此，可以通过气体与壁面的接触情况判断是否发生分离，当几何壁面表面剪应力$ {\tau }_{{\rm{w}}}\leqslant 0 $时，代表流体已经产生分离. 因此，确定壁面剪应力的分布情况就能确定来流与壁面的分离情况，图7为基于FLUENT计算结果绘出的壁面剪应力分布情况.

图 7 各工况在过渡段前后水平剪应力分布

Figure 7. Distribution of horizontal shear stress before and after transition section in each working condition

下载: 全尺寸图片幻灯片

由图7可知：1）在平板风场中，$ {\tau }_{{\rm{w}}} $沿程基本保持不变. 2） 3类被过渡段线型工况中，$ {\tau }_{{\rm{w}}} $曲线在距离设置的过渡段起点较远的距离就开始远离参考风场的剪应力曲线；剪应力在到达过渡段前沿程分布基本重合，到达过渡段后剪应力曲线开始产生分化，数值在一段区间内继续减小后迅速增大，超过参考风场的剪应力，达到最大点后又快速降低，回到参考风场工况附近. 3）总体上看，3类过渡段工况的沿程剪应力变化曲线变化趋势相近，而流经过渡段时，$ {\tau }_{\rm{w}} $波动的陡峭程度不同，出现向上增长、向下回归的先后次序也不同. 4）采用兰金物体绕流流线作为过渡段的工况B和采用平方正弦函数作为过渡段的工况D，$ {\tau }_{\rm{w}} $沿程未出现负值，即没有出现流动分离，2个工况$ {\tau }_{\rm{w}} $延程波动幅度都较小，而工况D的$ {\tau }_{\rm{w}} $波动程度相较工况B更小一些. 采用双曲正切函数作为过渡段的工况C，$ {\tau }_{\rm{w}} $在过渡段开始的一段距离出现负值，发生了流动分离，且$ {\tau }_{\rm{w}} $沿程波动剧烈，波动幅度较大.

过渡段线型的不同是造成上述差异的原因：1）对于双曲正切函数，其在连接边界严格满足式（2），过渡段曲线在开头处斜率较小，而在中间段距离内陡然增加，斜率较大；过渡段结尾接头处斜率又较小，曲线平缓；相应的双曲正切函数工况B中的$ {\tau }_{\rm{w}} $在初始过渡段平缓增长，而后流体在较短距离内较快抬升，对应部分的$ {\tau }_{\rm{w}} $快速增大，后快速回落，而后又经过较长较平缓的阶段. 2）对于平方正弦函数，其连接边界条件仅满足式（2）中的前2项，但其斜率变化平缓、分布均匀；相应的工况D中平方正弦的$ {\tau }_{\rm{w}} $在过渡段各阶段波动幅度较小；对于兰金物体绕流流线，其在连接边界基本满足式（2），各段斜率变化较双曲正切函数均匀一些，但不如平方正弦函数；相应的工况B中兰金物体绕流流线的$ {\tau }_{\rm{w}} $在过渡段波动程度较工况C小，波动幅度和工况D基本一致.

4.2 气流经过过渡段后平均风速的沿程分布

本节主要考察不同过渡段线型中沿程平均风特性变化情况，并与平板参考风场对照后，进一步评判各类过渡段曲线的优劣.

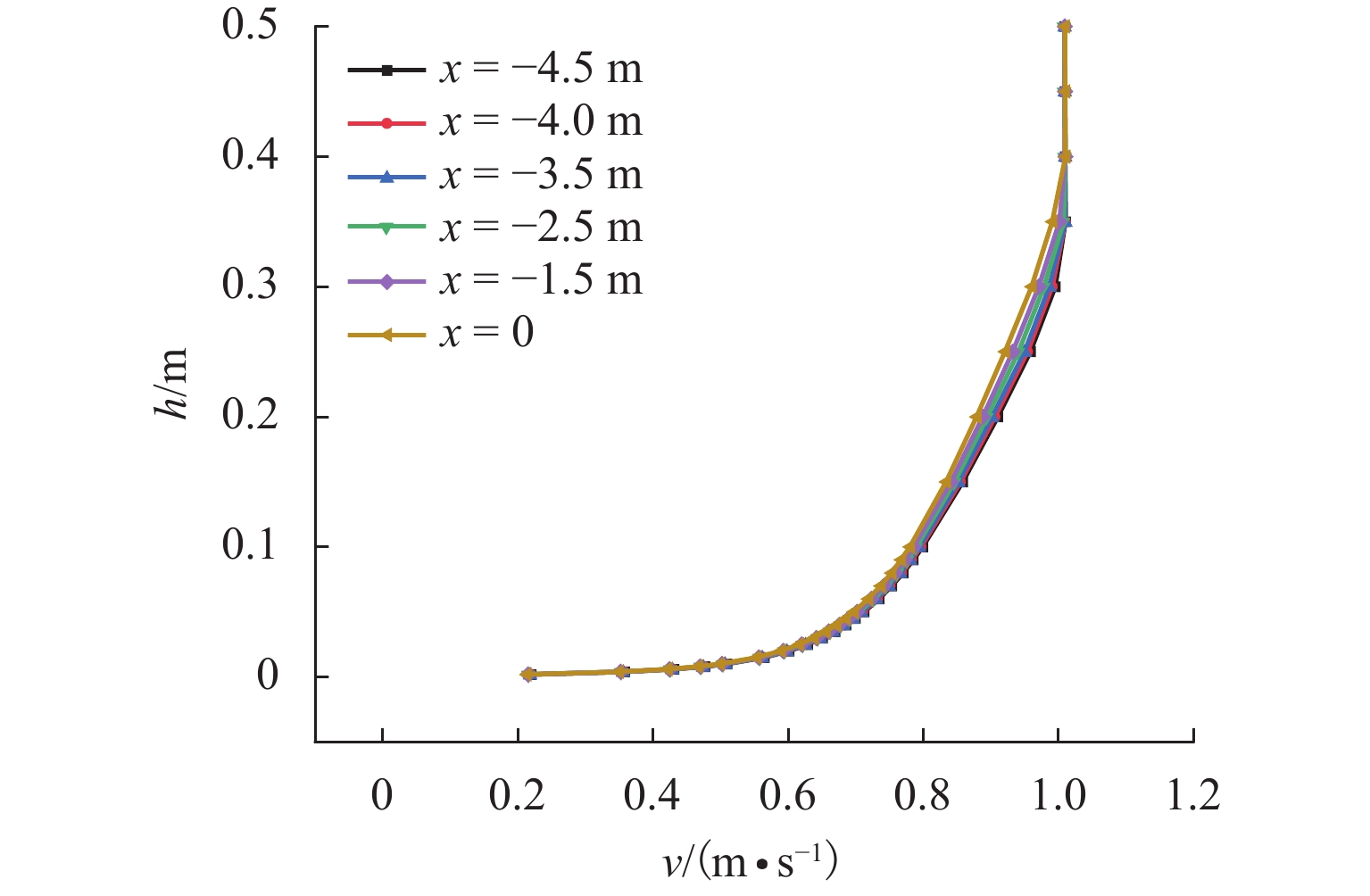
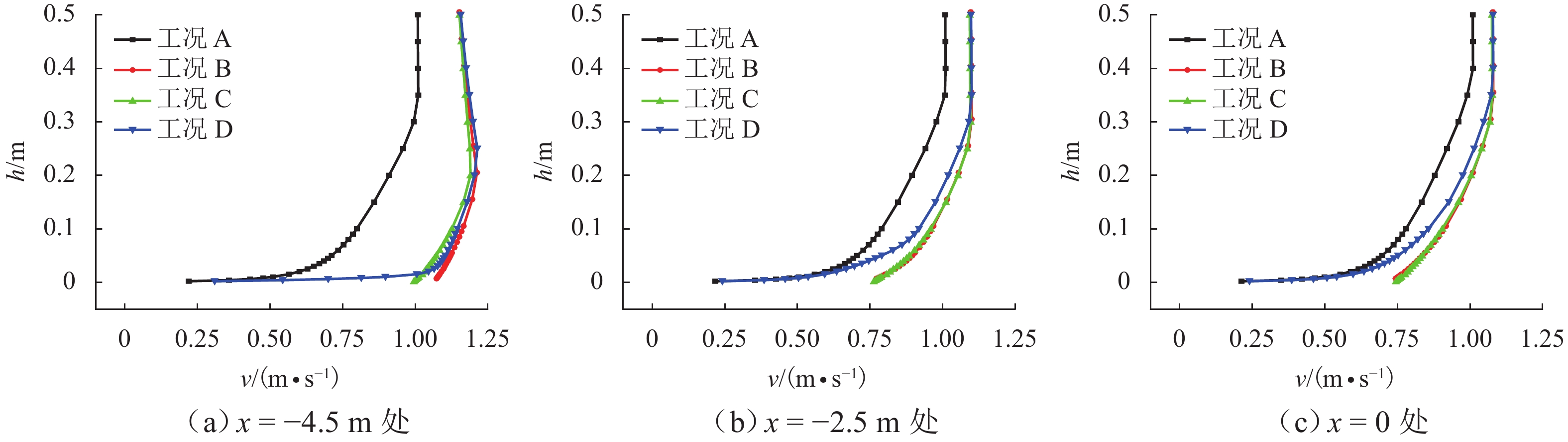
参考风场工况在典型监测位置处的风剖面如图8所示. 图中，v为风速. 由图可见：沿程不同位置处的风剖面已基本重合，这说明平板边界层风场已经充分发展、基本稳定，可作为参考风场. 不同过渡段曲线下，典型监测位置处的风剖面如图9所示.

图 8 平板参考风场沿程不同位置处风剖面

Figure 8. Wind profiles at different positions of plane reference wind field

下载: 全尺寸图片幻灯片

图 9 不同位置处各工况平均风剖面对比

Figure 9. Comparison of average wind profiles at different locations under each working condition

下载: 全尺寸图片幻灯片

由图9可见：1）随着流动沿程发展，各过渡段工况的风剖面和参考风场风剖面的差距逐渐缩小，但直到模型中心位置（x=0）处，各过渡段工况与平板参考风场仍有一定的差距. 2）在不同位置处的风剖面均有平方正弦函数（工况D）与参考风场的差距最小，工况B、C与参考风场的差距较大，且两工况基本重合. 3）工况B、C、D的梯度风速基本一致，风剖面在距离壁面较远处趋于重合. 4）在距离壁面较近处工况D的风剖面和参考风场重合，在壁面附近风速较小，随着流体远离过渡段，重合的部分增多；工况B、C的风剖面在壁面附近处风速较大，随着远离过渡段，风速有一定的减小，显然和参考风场差距较大.

采用平方正弦函数作为过渡段曲线时，在平均风剖面的保持方面性能较采用兰金物体绕流流线和双曲正切函数效果更优. 其原因在于：平方正弦函数的导函数即斜率沿程分布较均匀，曲线变化较平缓，对来流的扰动较小，没有发生流动分离，实现了气流的平稳过渡.

4.3 气流经过过渡段后风攻角的沿程分布

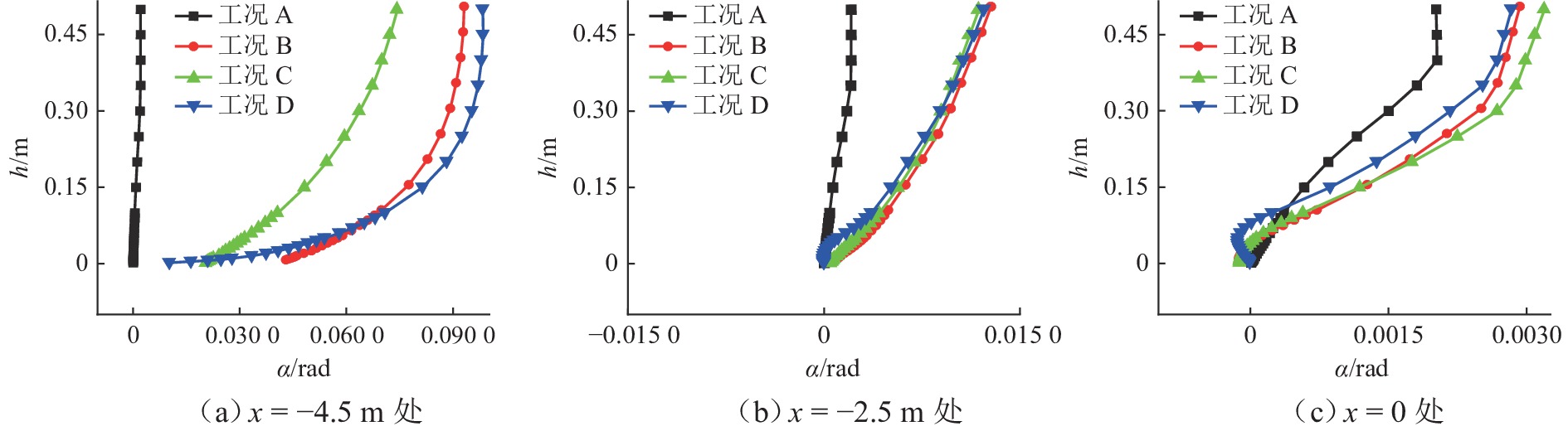
各工况在典型监测位置处的风攻角$\alpha $剖面如图10所示.

图 10 不同位置处各工况风攻角剖面对比

Figure 10. Comparison of wind attack angle profiles at different locations under each working condition

下载: 全尺寸图片幻灯片

由图10可知：1）参考风场的风攻角基本为0；2）随着来流沿过渡段流动，3类过渡段工况的风攻角逐渐减小；3）随着距离壁面高度的增加，风攻角逐渐增大，增大到一定程度后，保持不变；4）在接近过渡段终点的位置处，工况C的风攻角剖面较工况B、D更为接近参考风场，这显然是由于工况C的过渡段在接头处平缓段较长的原因；5）对于工况D，在距离壁面较近的一段，风攻角始终保持为0，这说明来流经过平方正弦曲线过渡后，边界层内始终保持为层流.

4.4 气流经过过渡段后湍流动能的沿程分布

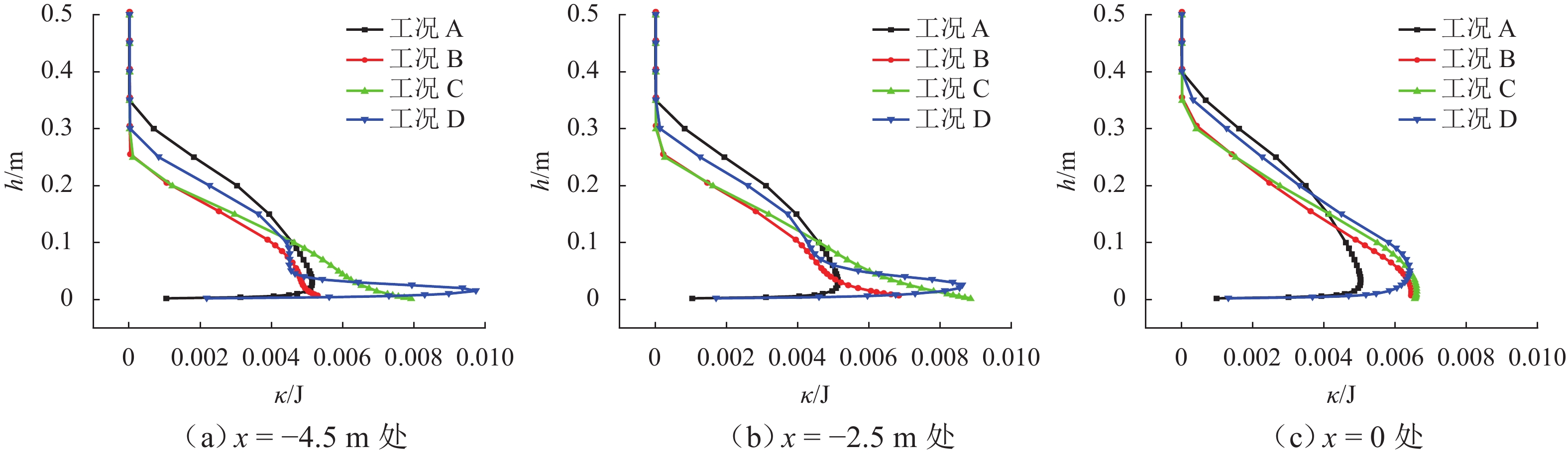
本节通过考察不同过渡段线型中沿程湍流动能$\kappa $的变化规律（图11所示），以来流流经过渡段后产生流动分离时流体的稳定程度为标准进一步评判各类过渡段曲线的优劣.

图 11 不同位置处各工况湍流动能对比

Figure 11. Comparison of turbulent kinetic energy at different locations under each working condition

下载: 全尺寸图片幻灯片

由图11可见：1）随着距离壁面高度的增加，各工况湍流动能基本重合且趋近于0. 2）平板参考风场（工况A）距离壁面相同高度处湍流动能沿程变化较小，比较平稳，沿高度变化为先增后减，最终趋于平稳. 3）在贴近壁面的区域，除工况B在流经过渡段后湍流动能在平台初段有所增加外，各过渡段工况沿程湍动能度逐渐减少，来流流动分离后转捩成湍流的部分逐渐降低. 这是来流流经过渡段后接触平直壁面时沿程流速逐渐下降，同距离壁面较高处风速差有所提高而引起的. 4）对于工况B、C，湍流动能沿高度变化趋势为逐渐降低，与平板参考风场变化趋势不同. 5）对于工况D，湍流动能沿程变化较大，但来流流经过渡段后变化趋势与参考风场工况比较贴合.

5. 结　论

1）以桥位为中心截取部分地形进行风场流动模拟，对于造成的台阶问题，可采取添加地形边界过渡段的形式加以解决.

2）构造地形模型边界过渡段线型宜遵循以下2个原则：其一是过渡段曲线本身满足二阶导函数连续，在连接边界处满足一阶导函数连续；其二是过渡段曲线一阶导函数即斜率应沿程分布较均匀，避免出现较大的窄带尖峰.

3）在可以作为过渡段曲线线型的兰金物体绕流流线、双曲正切函数和平方正弦函数中，平方正弦函数曲线绕流性能最优，可作为合理的过渡段曲线线型被选用进行桥址区风场模拟.

本文尚存在一些不足之处，研究工作均基于数值模拟开展，后续将通过风洞试验加以验证.

参考文献(15)

叶沅鑫,单杰,彭剑威,等. 利用局部自相似进行多光谱遥感影像自动配准[J]. 测绘学报,2014,43(3):268-275. YE Yuanxin, SHAN Jie, PENG Jianwei, et al. Automated multispectral remote sensing image registration using local self-similarity[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3):268-275.

张帅毅,李永树,蔡国林. 基于贝叶斯决策的航空影像自动配准[J]. 西南交通大学学报,2015,50(1):161-166. ZHANG Shuaiyi, LI Yongshu, CAI Guolin. Aerial image registration based on Bayesian decision theory[J]. Journal of Southwest Jiaotong University, 2015, 50(1):161-166.

YE Yuanxin, SHEN Li, WANG Jicheng, et al. Automatic matching of optical and SAR imagery through shape property[C]//2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS).:IEEE, 2015:1072-1075.

叶沅鑫,单杰,熊金鑫,等. 一种结合SIFT和边缘信息的多源遥感影像匹配方法[J]. 武汉大学学报:信息科学版,2013,38(10):1148-1151. YE Yuanxin, SHAN Jie, XIONG Jinxin, et al. A matching method combining SIFT and edge information for multi-source remote sensing images[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10):1148-1151.

ZITOV B, FLUSSER J. Image registration methods:a survey[J]. Image Vis. Comput., 2003, 21(11):977-1000.

YE Yuanxin, SHAN Jie. A local descriptor based registration method for multispectral remote sensing images with non-linear intensity differences[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 90:83-95.

SMITH S, BRADY J. SUSAN:a new approach to low level image processing[J]. International Journal of Computer Vision, 1997, 23(1):45-78.

LINDEBERG T. Feature detection with automatic scale selection[J]. International Journal of Computer Vision, 1998, 30(2):79-116.

MIKOLAJCZYK K, SCHMID C. Scale affine invariant interest point detectors[J]. International Journal of Computer Vision, 2004, 60(1):63-86.

MIKOLAJCZYK K, TUYTELAARS T, SCHMID C, et al. A comparison of affine region detectors[J]. International Journal of Computer Vision, 2005, 65(1):43-72.

LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2):91-110.

MATAS J, CHUM O, URBAN M, et al. Robust wide-baseline stereo from maximally stable extremal regions[J]. Image and Vision Computing, 2004, 22(10):761-767.

TUYTELAARS T, MIKOLAJCZYK K. Local invariant feature detectors:a survey[J]. Foundations and Trends in Computer Graphics and Vision, 2008, 3(3):177-280.

SCHMID C, MOHR R, BAUCKHAGE C. Evaluation of interest point detectors[J]. International Journal of Computer Vision, 2000, 37(2):151-172.

AANS H, DAHL A L, STEENSTRUP PEDERSEN K. Interesting interest points[J]. International Journal of Computer Vision, 2011, 97(1):18-35.

施引文献

附加材料(0)

访问统计